如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.
(1)设Rt△CBD的面积为S1,Rt△BFC的面积为S2,Rt△DCE的面积为S3,则S1 S2+S3(用“>”、“=”、“<”填空);
(2)写出如图中的三对相似三角形,并选择其中一对进行证明.
在矩形ABCD中,AB=a,AD=b,点M为BC边上一动点(点M与点B、C不重合),连接AM,过点M作MN⊥AM,垂足为M,MN交CD或CD的延长线于点N.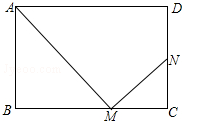
(1)求证:△CMN∽△BAM;
(2)设BM=x,CN=y,求y关于x的函数解析式.当x取何值时,y有最大值,并求出y的最大值;
(3)当点M在BC上运动时,求使得下列两个条件都成立的b的取值范围:①点N始终在线段CD上,②点M在某一位置时,点N恰好与点D重合.
已知⊙O是以AB为直径的△ABC的外接圆,OD∥BC交⊙O于点D,交AC于点E,连接AD、BD,BD交AC于点F.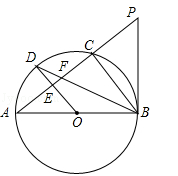
(1)求证:BD平分∠ABC;
(2)延长AC到点P,使PF=PB,求证:PB是⊙O的切线;
(3)如果AB=10,cos∠ABC=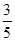 ,求AD.
,求AD.
过点(0,﹣2)的直线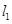 :
: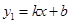 (
(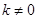 )与直线
)与直线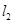 :
: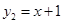 交于点P(2,m).
交于点P(2,m).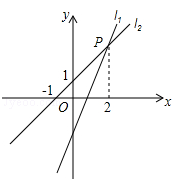
(1)写出使得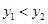 的x的取值范围;
的x的取值范围;
(2)求点P的坐标和直线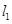 的解析式.
的解析式.
如图,在▱ABCD中,E、F为对角线AC上的两点,且AE=CF,连接DE、BF,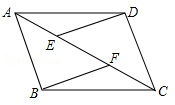
(1)写出图中所有的全等三角形;
(2)求证:DE∥BF.
已知购买1个足球和1个篮球共需130元,购买2个足球和1个篮球共需180元.
(1)求每个足球和每个篮球的售价;
(2)如果某校计划购买这两种球共54个,总费用不超过4000元,问最多可买多少个篮球?