如图所示,已知三棱柱ABC A1B1C1,
A1B1C1,
(1)若M、N分别是AB,A1C的中点,求证:MN∥平面BCC1B1;
(2)若三棱柱ABC A1B1C1的各棱长均为2,∠B1BA=∠B1BC=60°,P为线段B1B上的动点,当PA+PC最小时,求证:B1B⊥平面APC.
A1B1C1的各棱长均为2,∠B1BA=∠B1BC=60°,P为线段B1B上的动点,当PA+PC最小时,求证:B1B⊥平面APC.
已知函数 .
.
(1)当 时,求函数
时,求函数 在
在 上的值域;
上的值域;
(2)设 ,若存在
,若存在 ,使得以
,使得以 为三边长的三角形不存在,求实数
为三边长的三角形不存在,求实数 的取值范围.
的取值范围.
己知集合 ,
, ,
,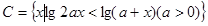 ,若“
,若“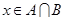 ”是“
”是“ ”的充分不必要条件,求
”的充分不必要条件,求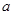 的取值范围.
的取值范围.
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和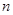 个黑球(
个黑球(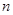 为正整数).现从甲、乙两个盒内各任取2个球,若取出的4个球均为黑球的概率为
为正整数).现从甲、乙两个盒内各任取2个球,若取出的4个球均为黑球的概率为 ,求
,求
(1)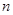 的值;
的值;
(2)取出的4个球中黑球个数大于红球个数的概率.
已知 为单调递增的等比数列,且
为单调递增的等比数列,且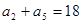 ,
,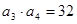 ,
,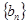 是首项为2,公差为
是首项为2,公差为 的等差数列,其前
的等差数列,其前 项和为
项和为 .
.
(1)求数列 的通项公式;
的通项公式;
(2)当且仅当 ,
, ,
,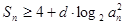 成立,求
成立,求 的取值范围.
的取值范围.
在 中,角
中,角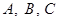 所对的边分别为
所对的边分别为 ,且
,且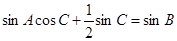 .
.
(1)求 的大小;
的大小;
(2)若 是锐角三角形,且
是锐角三角形,且 ,求
,求 周长
周长 的取值范围.
的取值范围.