一台机床有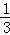 的时间加工零件A,其余时间加工零件B,加工零件A时,停机的概率为
的时间加工零件A,其余时间加工零件B,加工零件A时,停机的概率为 ,加工零件B时,停机的概率是
,加工零件B时,停机的概率是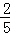 ,则这台机床停机的概率为()
,则这台机床停机的概率为()
A.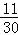 |
B.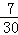 |
C.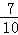 |
D.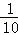 |
若某射击手每次射击击中目标的概率为P(0<P<1),每次射击的结果相互独立,在他连续8次射击中,“恰有3次击中目标”的概率是“恰有5次击中目标”的概率的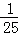 ,则P的值为()
,则P的值为()
A.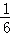 |
B. |
C.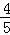 |
D.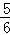 |
同时抛掷两枚质地均匀的硬币,则出现两个正面朝上的概率是()
A.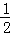 |
B. |
C. |
D. |
在三次独立重复试验中,事件A在每次试验中发生的概率相同,若事件A至少发生一次的概率为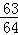 ,则事件A恰好发生一次的概率为()
,则事件A恰好发生一次的概率为()
A.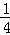 |
B.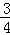 |
C.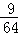 |
D. |
设两个独立事件A,B都不发生的概率为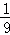 .则A与B都发生的概率值可能为()
.则A与B都发生的概率值可能为()
A. |
B.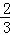 |
C. |
D.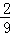 |