如图所示,一定滑轮上绕有轻质柔软细线,线的一端系一质量为3m的重物,另一端系一质量为m、电阻为r的金属杆。在竖直平面内有间距为L的足够长的平行金属导轨PQ、EF,在QF之间连接有阻值为R的电阻,其余电阻不计,磁感应强度为B0的匀强磁场与导轨平面垂直。开始时金属杆置于导轨下端QF处,将重物由静止释放,当重物下降h时恰好达到稳定速度而匀速下降。运动过程中金属杆始终与导轨垂直且接触良好,(忽略摩擦阻力,重力加速度为g),则
A.电阻R中的感应电流方向Q F F |
B.重物匀速下降的速度 |
| C.重物从释放到下降h的过程中,重物机械能的减少量大于回路中产生的焦耳热 |
D.若将重物下降h时的时刻记作t=0,速度记为v0,从此时刻起,磁感应强度逐渐减小,使金属杆中恰好不再产生感应电流,则磁感应强度B随时间t变化的关系式 |
根据图中的漫画,判断下列说法中正确的是( )
| A.人看到的是鱼的实像,位置变浅了些 |
| B.人看到的是鱼的虚像,位置变浅了些 |
| C.鱼看到的是人的实像,位置偏低了些 |
| D.鱼看到的是人的虚像,位置偏高了些 |
一列简谐横波沿直线传播,该直线上的a、b两点相距4.42 m.图中实、虚两条曲线分别表示平衡位置在a、b两点处质点的振动曲线.由此可知( )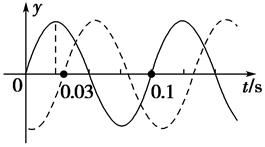
| A.此列波的频率一定是10 Hz |
| B.此列波的波长一定是0.1 m |
| C.此列波的传播速度一定是34 m/s |
| D.a点一定比b点距波源近 |
如下图所示,甲为沿x轴传播的一列简谐横波在t=0时刻的波动图象,乙图为参与波动质点P的振动图象,则下列判断正确的是( )
| A.该波的传播速率为4 m/s |
| B.该波的传播方向沿x轴正方向 |
| C.经过0.5 s时间,质点P沿波的传播方向向前传播2 m |
| D.该波在传播过程中若遇到8 m的障碍物,能发生明显衍射现象 |
先后用两种不同的单色光,在相同的条件下用同双缝干涉装置做实验,在屏幕上相邻的两条亮纹间距不同,其中间距较大的那种单色光,比另一种单色光()
| A.在真空中的波长较短 |
| B.在玻璃中传播的速度较大 |
| C.在玻璃中传播时,玻璃对其折射率较大 |
| D.其在空气中传播速度大 |
如图所示,一个三棱镜的截面为等腰直角△ABC,∠A为直角。此截面所在平面内的光线沿平行于BC边的方向射到AB边,进入棱镜后直接射到AC边上,并刚好能发生全反射。该棱镜材料的折射率为( )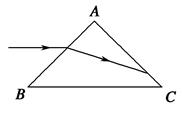
A.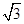 |
B. |
C.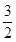 |
D.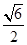 |