如图所示，倾角θ=300、长L=4.5m的斜面，底端与一个光滑的1/4圆弧轨道平
滑连接，圆弧轨道底端切线水平．一质量为m=1kg的物块（可视为质点）从斜面最高点A由静止开始沿斜面下滑，经过斜面底端B后恰好能到达圆弧轨道最高点C，又从圆弧轨道滑回，能上升到斜面上的D点，再由D点由斜面下滑沿圆弧轨道上升，再滑回，这样往复运动，最后停在B点．已知物块与斜面间的动摩擦因数为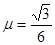
，g=10m/s2，假设物块经过斜面与圆弧轨道平滑连接处速率不变．求：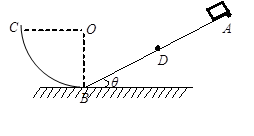
⑴.物块经多长时间第一次到B点；
⑵.物块第一次经过B点时对圆弧轨道的压力；
⑶.物块在斜面上滑行的总路程．
如图所示，M、N为水平放置、互相平行的两大块金属板，间距d="35" cm，已知N板电势高，两板间电压U=3.5×104 V。现有一质量m=7.0×10－6 kg，电荷量q=6.0×10－10 C的带负电的油滴，由下板N下方距N为h="15" cm的O处竖直上抛，经N板中间的P孔进入电场，欲使油滴到达上板Q点时速度恰为零，问油滴上抛的初速度v0为多大?
如图所示，在xoy第一象限内分布有垂直xoy向外的匀强磁场，磁感应强度大小
。在第二象限紧贴y轴和x轴放置一对平行金属板MN（中心轴线过y轴），极板间距
；极板与左侧电路相连接，通过移动滑动头P可以改变极板MN间的电压。a、b为滑动变阻器的最下端和最上端（滑动变阻器的阻值分布均匀），a、b两端所加电压
。在MN中心轴线上距y轴距离为
处，有一粒子源S沿x轴正方向连续射出比荷为
，速度为
带正电的粒子，粒子经过y轴进入磁场，经过磁场偏转后从x轴射出磁场（忽略粒子的重力和粒子之间的相互作用）。
（1）当滑动头P在a端时，求粒子在磁场中做圆周运动的半径R0；
（2）当滑动头P在ab正中间时，求粒子射入磁场时速度的大小；
（3）滑动头P的位置不同则粒子在磁场中运动的时间也不同，求粒子在磁场中运动的最长时间。
如图所示，光滑水平轨道与半径为R的光滑竖直半圆轨道在B点平滑连接。在过圆心O的水平界面MN的下方分布有水平向右的匀强电场。现有一质量为m，电量为+q的小球从水平轨道上A点由静止释放，小球运动到C点离开圆轨道后，经界面MN上的P点进入电场（P点恰好在A点的正上方，如图。小球可视为质点，小球运动到C点之前电量保持不变，经过C点后电量立即变为零）。已知A、B间距离为2R，重力加速度为g。在上述运动过程中，求：
（1）电场强度E的大小；
（2）小球在圆轨道上运动时最大速率；
（3）小球对圆轨道的最大压力的大小。
如图所示，倾角为30°的光滑斜面与粗糙的水平面平滑连接。现将一滑块（可视为质点）从斜面上A点由静止释放，最终停在水平面上的C点。已知A点距水平面的高度h=0.8m，B点距C点的距离L=2.0m。（滑块经过B点时没有能量损失，g=10m/s2），求：
（1）滑块在运动过程中的最大速度；
（2）滑块与水平面间的动摩擦因数μ；
（3）滑块从A点释放后，经过时间t=1.0s时速度的大小。
某课外小组经长期观测，发现靠近某行星周围有众多卫星，且相对均匀地分布于行星周围，假设所有卫星绕该行星的运动都是匀速圆周运动，通过天文观测，测得离行星最近的一颗卫星的运动半径为R1，周期为T1，已知万有引力常为G。求：
⑴行星的质量；
⑵若行星的半径为R，行星的第一宇宙速度；
⑶通过天文观测，发现离行星很远处还有一颗卫星，其运动半径为R2，周期为T2，试估算靠近行星周围众多卫星的总质量。