已知椭圆E：
＋y2＝1(a＞1)的上顶点为M(0，1)，两条过M的动弦MA、MB满足MA⊥MB.
(1)当坐标原点到椭圆E的准线距离最短时，求椭圆E的方程；
(2)若Rt△MAB面积的最大值为
，求a；
(3)对于给定的实数a(a＞1)，动直线AB是否经过一定点？如果经过，求出定点坐标(用a表示)；反之，说明理由．
（本小题满分12分）
设数列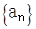
的前n项和为
且方程
有一根为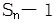
，n=1,2,3…,试求
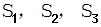的值，猜想的表达式，并用数学归纳法加以证明
（本小题满分12分）
某商场从生产厂家以每件20元的价格购进一批商品，该商品的销售量Q（单位：
件）与零售价p（单位：元）有如下关系为
Q=8300-170p-
,求该商品零售价定为多少元时，毛利润L最大，并求出最大毛利润（毛利润=销售收入-进货支出）
（本小题满分12分）
若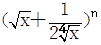
的展开式中前三项系数成等差数列，求：
（1）展开式中所有的有理项
（2）展开式中系数最大项
（本小题满分12分）
已知曲线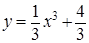
(1)求曲线在点P(2,4)处的切线方程
(2)求曲线在点P(2,4)的切线方程
(3)求斜率为4的曲线的切线方程
（本小题满分12分）
已知复数w满足w-4=(3-2w)i(i为虚数单位)，
,求