如图,虚线框内为改装好的电表,M、N为新电表的接线柱,其中灵敏电流计G的满偏电流为200μA,已测得它的内阻为495.0Ω。图中电阻箱读数为5.0Ω。现将MN接入某电路,发现灵敏电流计G刚好满偏,则根据以上数据计算可知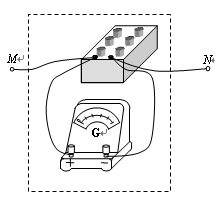
| A.M、N两端的电压为1mV |
| B.M、N两端的电压为100mV |
| C.流过M、N的电流为2μA |
| D.流过M、N的电流为20mA |
物理学是建立在实验基础上的一门学科,很多定律是可以通过实验进行验证的。下列定律中不能通过实验直接得以验证的是()
| A.牛顿第一定律 | B.楞次定律 | C.电阻定律 | D.库仑定律 |
如图所示,波源S从平衡位置y=0开始振动,运动方向竖直向上(y轴的正方向),振动周期T=0.01s,产生的机械波向左、右两个方向传播,波速均为v=80m/s,经过一段时间后,P、Q两点开始振动,已知距离SP=1.2m、SQ=2.6m.若以Q点开始振动的时刻作为计时的零点,则在下图所示的四幅振动图象中,能正确描述S、P、Q三点振动情况的是

| A.甲为Q点的振动图象 | B.乙为振源S点的振动图象 |
| C.丙为P点的振动图象 | D.丁为P点的振动图象 |
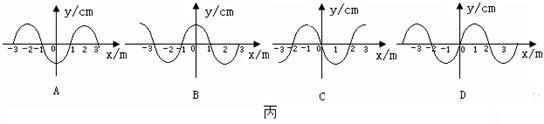
已知平面简谐波在x轴上传播,原点O的振动图线如图甲所示,在t时刻的波形图如图乙所示,则t’=t+0.5s时刻的波形图线可能是图丙中的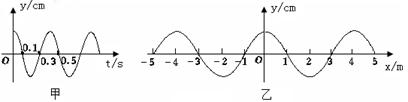
如图所示,一轻质弹簧竖直放置,下端固定在水平面上,上端处于a位置,当一重球放在弹簧上端静止时,弹簧上端被压缩到b位置。现将重球(视为质点)从图示c位置沿弹簧中轴线自由下落,弹簧被重球压缩到最低位置d。以下关于重球运动过程的正确说法应是
| A.重球下落压缩弹簧由a至d的过程中,重球做减速运动 |
| B.由a至d过程中重球克服弹簧弹力做的功等于小球由c下落至d处时重 力势能减少量 |
| C.重球下落至d处获得最大加速度a>g |
| D.要使重球在接下去的运动中不脱离弹簧,小球释放的位置的高度不能超过a点的高度 |
在张紧的绳子上挂了a、b、c、d四个单摆,摆长关系为Lc > Lb = Ld > La,如图所示,先让d摆动起来(摆角不超过10°,d摆球的质量远大于其它摆球)则下列说法正确的是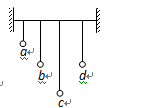
| A.b摆发生振动其余摆均不动 | B.所有的摆均以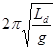 的周期振动 的周期振动 |
| C.所有的摆均以相同摆角振动 | D.a、b、c中b摆振动幅度最大 |