1885年瑞士的中学教师巴耳末发现,氢原子光谱中可见光部分的四条谱线的波长可归纳成一个简单的经验公式: ,n为大于2的整数,R为里德伯常量。1913年,丹麦物理学家玻尔受到巴耳末公式的启发,同时还吸取了普朗克的量子假说、爱因斯坦的光子假说和卢瑟福的核式结构原子模型,提出了自己的原子理论。根据玻尔理论,推导出了氢原子光谱谱线的波长公式:
,n为大于2的整数,R为里德伯常量。1913年,丹麦物理学家玻尔受到巴耳末公式的启发,同时还吸取了普朗克的量子假说、爱因斯坦的光子假说和卢瑟福的核式结构原子模型,提出了自己的原子理论。根据玻尔理论,推导出了氢原子光谱谱线的波长公式: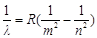 ,m与n都是正整数,且n > m。当m取定一个数值时,不同数值的n得出的谱线属于同一个线系。如:
,m与n都是正整数,且n > m。当m取定一个数值时,不同数值的n得出的谱线属于同一个线系。如:
m=1,n=2、3、4、…组成的线系叫赖曼系;
m=2,n=3、4、5、…组成的线系叫巴耳末系;
m=3,n=4、5、6、…组成的线系叫帕邢系;
m=4,n=5、6、7、…组成的线系叫布喇开系;
m=5,n=6、7、8、…组成的线系叫逢德系。
以上线系只有一个在紫外光区,这个线系是
| A.赖曼系 | B.帕邢系 | C.布喇开系 | D.逢德系 |
两大小相同的实心小铁球紧靠在一起,它们之间的万有引力为F,若两个半径是小铁球2倍的实心大铁球紧靠在一起,则它们之间的万有引力为 ( )
| A.2F | B.4F | C.8F | D.16F |
球A和球B可在光滑杆上无摩擦滑动,两球用一根细绳连接如右图所示,球A的质量是球B的两倍,当杆以角速度ω匀速转动时,两球刚好保持与杆无相对滑动,那么 ( )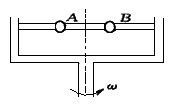
| A.球A受到的向心力大于B受到的向心力 |
| B.球A转动的半径是球B转动半径的一半 |
| C.当A球质量增大时,球A向外运动 |
| D.当ω增大时,球B向外运动 |
如图所示,A.B两个小球,质量相等,用一根轻绳相连,另有一根轻绳的两端分别连接O点和B球,让两小球绕O点在光滑水平桌面上以相同的角速度做匀速圆周运动,若OB绳上的拉力为F1,AB绳上的拉力为F2,OB=2AB,则 ( )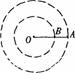
A.F1:F2=2:3 B.F1:F2=3:2 C.F1:F2=5:3 D.F1:F2=2:1
如下图所示,O1为皮带传动的主动轮的轴心,轮半径为r1.O2为从动轮的轴心,轮半径为r2.r3为固定在从动轮上的小轮半径.已知r2=2rI,r3=1.5rl,A.B.C分别是3个轮边缘上的点,则质点A.B.C的向心加速度之比是(皮带不打滑) ( )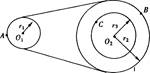
A.1:2:3 B.2:4:3 C.8:4:3 D.3:6:2
在曲线运动中,如果速率保持不变,那么运动物体的加速度 ( )
| A.加速度的方向就是曲线这一点的的切线方向 |
| B.加速度大小不变,方向与物体运动方向一致 |
| C.加速度大小不变,某点的加速度方向与曲线该点的切线方向一致 |
| D.加速度大小和方向由物体在该点所受合外力决定,方向与曲线这一点的的切线方向垂直 |