已知 、
、 为椭圆
为椭圆 的左、右焦点,且点
的左、右焦点,且点 在椭圆
在椭圆 上.
上.
(1)求椭圆 的方程;
的方程;
(2)过 的直线
的直线 交椭圆
交椭圆 于
于 两点,则
两点,则 的内切圆的面积是否存在最大值,若存在其最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值,若存在其最大值及此时的直线方程;若不存在,请说明理由.
(本小题满分12分)
已知等差数列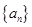 满足
满足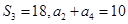 。
。
(Ⅰ)求通项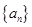 的通项公式及
的通项公式及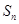 的最大值;
的最大值;
(Ⅱ)设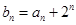 ,求数列
,求数列 的其前
的其前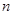 项和
项和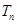 .
.
(本小题14分)某人有楼房一幢,室内面积共计180m2,拟分割成两类房间作为旅游客房,大房间每间面积为18m2,可住游客5名,每名游客每天住宿费40元;小房间每间面积为15m2,可以住游客3名,每名游客每天住宿费50元;装修大房间每间需要1000元,装修小房间每间需要600元.如果他只能筹款8000元用于装修,且游客能住满客房,他应隔出大房间和小房间各多少间,每天能获得最大的房租收益?(注:设分割大房间为x间,小房间为y间,每天的房租收益为z元)
(1)写出x,y所满足的线性约束条件;
(2)写出目标函数的表达式;
(3)求x,y各为多少时,每天能获得最大的房租收益?每天能获得最大的房租收益是多少?
(本小题12分)运货卡车以每小时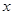 千米的速度匀速行驶130千米
千米的速度匀速行驶130千米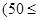
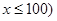 (单位:千米/小时).假设汽油的价格是每升2a元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升2a元,而汽车每小时耗油 升,司机的工资是每小时14a元.(1)求这次行车总费用
升,司机的工资是每小时14a元.(1)求这次行车总费用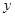 关于
关于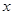 的表达式;(2)当
的表达式;(2)当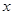 为何值时,这次行车的总费用最低,并求出最低费用的值(a为常数) .
为何值时,这次行车的总费用最低,并求出最低费用的值(a为常数) .
(本小题12分)等差数列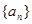 的前
的前 项和记为
项和记为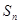 ,已知
,已知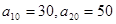 .
.
(1)求数列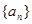 的通项
的通项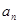 ;(2)若
;(2)若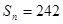 ,求
,求 ;(3)令
;(3)令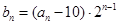 ,求数列
,求数列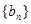 的前
的前 项和
项和 .
.
(本小题12分)ΔABC中A,B,C的对边分别为a,b,c,且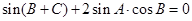
求:(1)角B的大小;(2)若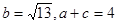 ,求ΔABC的面积.
,求ΔABC的面积.