如图所示，A为太阳系中的天王星，它绕太阳O运行的轨道视为圆时，运动的轨道半径为R0，周期为T0。长期观测发现，天主星实际运动的轨道与圆轨道总有一些偏离，且每隔t0时间发生一次最大偏离，即轨道半径出现一次最大。根据万有引力定律，天文学家预言形成这种现象的原因可能是夭王星外侧还存在着一颗未知的行星(假设其运动轨道与A在同一平面内，且与A的绕行方向相同），它对天王星的万有引力引起天王星轨道的偏离，由此可推测未知行星的运动轨道半径是
一个质量为25Kg的小孩从高度为3m的滑梯顶端由静止开始滑下，滑到底端的速度为2m/s，g取10m/s2,关于力对小孩做的功，结论正确的是：
| A．合外力做功50J | B．阻力做功-50J | C．重力做功50J | D．支持力做功50J |
物体在运动过程中，克服重力做功50J，则
| A．物体的重力势能可能不变 | B．物体的重力势能一定减小50J |
| C．物体的重力势能一定增加50J | D．物体的重力一定做功50J |
假设汽车以额定功率在水平路面上行驶，所受阻力保持不变，则它可能做：
| A．匀加速直线运动 | B．匀减速直线运动 | C．匀速直线运动 | D．变加速直线运动 |
如图，滑雪者由静止沿斜坡从A点自由滑下，然后在水平地面上前进至B点停下，已知斜坡、水平面和滑雪者之间的动摩擦因素皆为μ，滑雪者（包括滑雪板）的质量为m，A、B两点间水平距离为L，A、C之间的距离为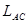
，B、C之间的距离
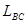，在滑雪者经过AB段过程中，克服摩擦力做的功为：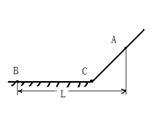
A. 大于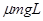
B.等于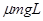
C.小于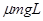
D.等于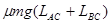
物体沿斜面匀速上升的过程中，它的：
| A．动能减小，势能不变 | B．动能不变，势能增加 |
| C．动能减小，势能不变 | D．动能不变，势能减小 |