已知函数f(x)在R上满足f(x)＝2f(2－x)－x2＋8x－8，则曲线y＝f(x)在点(1，f(1))处的切线方程是( )
| A．y＝2x－1 | B．y＝x | C．y＝3x－2 | D．y＝－2x＋3 |
设椭圆的两个焦点分别为F1，F2，过F2作椭圆长轴的垂线交椭圆于点P，若三角形F1PF2为等腰直角三角形，则椭圆的离心率为
A． |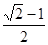
B． |
C． |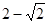
D． |
一个空间几何体的三视图如下，则它的体积是
A． |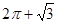
B． |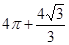
C． |
D． |
在平行四边形ABCD中，E、F分别是CD和BC的中点，若
，其中
，则
的值是
A． |
B．1 | C． |
D． |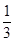
曲线
在横坐标为
的点处的切线为L，则点（3,2）到L的距离是
A． |
B． |
C． |
D． |
现要完成3项抽样调查：
①从10盒酸奶中抽取3盒进行卫生检查；
②科技报告厅有座椅32排，每排40个座位，有一次报告会恰好坐满了观众，抽取32位进行座谈；
③某中学共有160名教职工，其中教师120名，行政人员16名，后勤人员24名，为了解教职工对校务公开方面的意见，抽取一个容量为20的样本进行调查
| A．①简单随机抽样②系统抽样③分层抽样 | B．①简单随机抽样②分层抽样③系统抽样 |
| C．①系统抽样②简单随机抽样③分层抽样 | D．①分层抽样②系统抽样③简单随机抽样 |