为减少烟尘排放对空气的污染,某同学设计了一个如图所示的静电除尘器,该除尘器的上下底面是边长为L=0.20m的正方形金属板,前后面是绝缘的透明有机玻璃,左右面是高h=0.10m的通道口。使用时底面水平放置,两金属板连接到U=2000V的高压电源两极(下板接负极),于是在两金属板间产生一个匀强电场(忽略边缘效应)。均匀分布的带电烟尘颗粒以v=10m/s的水平速度从左向右通过除尘器,已知每个颗粒带电荷量 q=+2.0×10-17C,质量m=1.0×10-15kg,不考虑烟尘颗粒之间的相互作用和空气阻力,并忽略烟尘颗粒所受重力。在闭合开关后:
(1)求烟尘颗粒在通道内运动时加速度的大小和方向;
(2)求除尘过程中烟尘颗粒在竖直方向所能偏转的最大距离;
(3)除尘效率是衡量除尘器性能的一个重要参数。除尘效率是指一段时间内被吸附的烟尘颗粒数量与进入除尘器烟尘颗粒总量的比值。试求在上述情况下该除尘器的除尘效率;若用该除尘器对上述比荷的颗粒进行除尘,试通过分析给出在保持除尘器通道大小不变的前提下,提高其除尘效率的方法。
有若干相同的小钢球,从斜面上的某一位置每隔0.1s无初速地释放一颗,在连续释放若干颗钢球后,对准斜面上正在滚动的若干小球拍摄到如右图所示的照片,测得AB=25cm,BC=30cm。
求(1)拍摄 照片时B球的速度;
照片时B球的速度;
(2)A球上面还有几颗正在滚动的小钢球。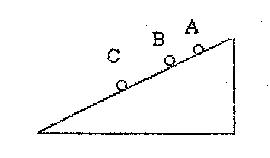
如图所示,质量为M的直角三棱柱A放在水平地面上,三棱柱的斜面是光滑的,且斜面倾角为θ。质量为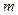 的光滑球放在三棱柱和光滑竖直墙壁之间,A和B都处于静止状态,求地面对三棱柱支持力和摩擦力各为多少?
的光滑球放在三棱柱和光滑竖直墙壁之间,A和B都处于静止状态,求地面对三棱柱支持力和摩擦力各为多少?
某人骑自行车以4m/s的速度匀速前进,某时刻在他正前方7m处以10m/s的速度同向行驶的汽车开始关闭发动机,然后以2m/s2的加速度匀减速前进,求此人需多长时间才能追上汽车?
如图16,一质量为m 的物块静止在桌面边缘,桌面离水平地面的高度为h。一质量也为m 的子弹以水平速度v0射入物块后,以水平速度v0/2射出,重力加速度为g。求:
(1)子弹射出瞬间物块的速度;
(2)子弹射穿物块过程中 系统损失的机械能;
系统损失的机械能;
(3)物块落地点离桌面边缘的水平距离. 
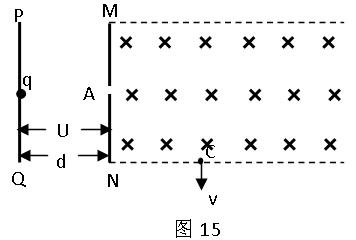
如图15所示,PQ、MN两极板间存在匀强电场,两极板间电势差为U、间距为d,MN极板右侧虚线区域内有垂直纸面向内的匀强磁场。现有一初速度为零、带电量为q、质量为m的离子从PQ极板出发,经电场加速后,从MN上的小孔A垂直进入磁场区域,并从C点垂直于虚线边界射出。求:
(1)离子从小孔A射出时速度v0;
(2)离子带正电还是负电?C点离MN板的距离?