已知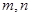 是不重合的直线,
是不重合的直线,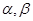 是不重合的平面,有下列命题:
是不重合的平面,有下列命题:
①若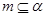 ,
, ∥
∥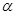 ,则
,则 ∥
∥ ;
;
②若 ∥
∥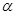 ,
, ∥
∥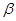 ,则
,则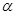 ∥
∥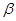 ;
;
③若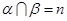 ,
, ∥
∥ ,则
,则 ∥
∥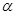 且
且 ∥
∥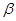 ;
;
④若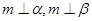 ,则
,则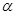 ∥
∥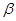
其中真命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |
“复数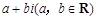 为纯虚数”是“
为纯虚数”是“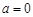 ”的( )
”的( )
| A.充分条件,但不是必要条件 | B.必要条件,但不是充分条件 |
| C.充要条件 | D.既不是充分也不是必要条件 |
图中所示的是一个算法的流程图.已知 ,输出的结果为
,输出的结果为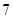 ,则
,则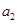 的值为()
的值为()
| A.12 | B.11 | C.10 | D.9 |
在建立两个变量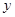 与
与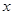 的回归模型中,分别选择了4个不同模型,他们的相关指数
的回归模型中,分别选择了4个不同模型,他们的相关指数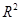 如下,其中拟合的最好的模型是()
如下,其中拟合的最好的模型是()
A.模型1的相关指数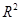 为 为 |
B.模型2的相关指数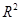 为 为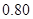 |
C.模型3的相关指数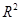 为 为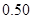 |
D.模型4的相关指数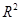 为 为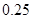 |
类比“等差数列的定义”给出一个新数列“等和数列的定义”是( )
| A.连续两项的和相等的数列叫等和数列 |
| B.从第二项起,以后每一项与前一项的差都不相等的数列叫等和数列 |
| C.从第二项起,以后每一项与前一项的和都相等的数列叫等和数列 |
| D.从第一项起,以后每一项与前一项的和都相等的数列叫等和数列 |
用演绎法证明函数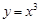 是增函数时的小前提是 ()
是增函数时的小前提是 ()
| A.增函数的定义 | B.函数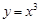 满足增函数的定义 满足增函数的定义 |
C.若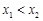 ,则 ,则 |
D.若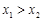 ,则 ,则 |