在一张矩形纸片上,画有一个圆(圆心为O)和一个定点F (F在圆外).在圆上任取一点M,将纸片折叠使点M与点F重合,得到折痕CD.设直线CD与直线OM交于点P,则点P的轨迹为
A.圆 B.椭圆 C.双曲线 D.直线
在棱长为2的正方体ABCD-A1B1C1D1中,点O为底面ABCD的中心,在正方体ABCD-A1B1C1D1内随机取一点P,则点P到点O的距离大于1的概率为(注:球的体积公式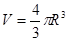 )
)
A.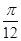 |
B.1-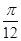 |
C.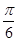 |
D.1-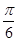 |
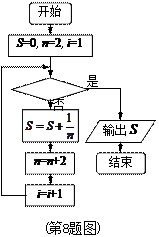
下图给出的是计算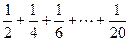 的值的一个程序框图,其中判断框内应填
的值的一个程序框图,其中判断框内应填
入的条件是
A.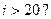 |
B.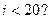 |
C.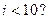 |
D.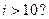 |
设圆锥曲线r的两个焦点分别为F1,F2,若曲线r上存在点P满足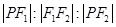 =4:3:2,则曲线r的离心率等于
=4:3:2,则曲线r的离心率等于
A.  |
B.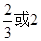 |
C.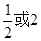 |
D. |
方程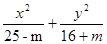 =1表示焦点在y轴上的椭圆,则m的取值范围是
=1表示焦点在y轴上的椭圆,则m的取值范围是
| A.-16<m<25 | B.-16<m<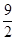 |
C.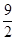 <m<25 <m<25 |
D.m>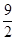 |