已知随机变量 的分布列是其中
的分布列是其中 ,则
,则
 |
-1 |
0 |
2 |
| P |
 |
 |
 |
A、 B、
B、 C、0 D、1
C、0 D、1
根据如下样本数据得到的回归方程为 =bx+a,则()
=bx+a,则()
| x |
3 |
4 |
5 |
6 |
7 |
8 |
| y |
4.0 |
2.5 |
-0.5 |
0.5 |
-2.0 |
-3.0 |
A.a>0,b<0 B.a>0,b>0C.a<0,b<0 D.a<0,b>0
有一段演绎推理:“直线平行于平面,则这条直线平行于平面内所有直线;已知直线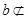 平面
平面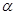 ,直线
,直线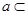 平面
平面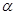 ,直线
,直线 ∥平面
∥平面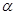 ,则直线
,则直线 ∥直线
∥直线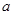 ”的结论是错误的,这是因为()
”的结论是错误的,这是因为()
| A.大前提错误 | B.小前提错误 |
| C.推理形式错误 | D.非以上错误 |
已知函数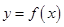 的导函数
的导函数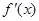 的图象如右图所示,则函数
的图象如右图所示,则函数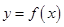 的图象可能是()
的图象可能是()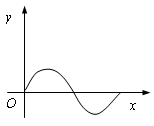
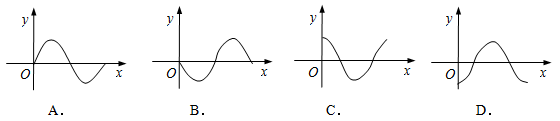
已知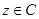 ,且
,且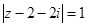 ,
,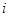 是虚数单位,则
是虚数单位,则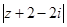 的最小值是()
的最小值是()
| A.2 | B.3 | C.4 | D.5 |