若直角坐标平面内的亮点P,Q满足条件: P,Q都在函数y=f(x)的图像上, P,Q关于原点对称,则称点对[P,Q]是函数y=f(x)的一对“友好点对”(点对[P,Q]与[Q,P]看作同一对“友好点对”)。
已知函数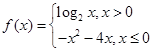 ,则此函数的“友好点对”有( )
,则此函数的“友好点对”有( )
| A.0对 | B.1对 | C.2对 | D.3对 |
甲、乙两队进行排球决赛,现在的情形是甲队只要再赢一局就获冠军,乙队需要再赢两局才能得冠军,若两队每局获胜的概率相同,则甲队获得冠军的概率为( )
A. |
B. |
C. |
D. |
一个篮球运动员投篮一次得3分的概率为a,得2分的概率为b,不得分的概率为c(a,b,c∈(0,1)),已知他投篮一次得分的均值为2,则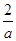 +
+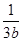 的最小值为( )
的最小值为( )
A.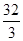 |
B.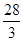 |
C.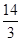 |
D.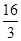 |
一袋中有5个白球,3个红球,现从袋中往外取球,每次任取一个记下颜色后放回,直到红球出现10次时停止,设停止时共取了ξ次球,则P(ξ=12)=( )
A.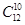 ( ( )10( )10( )2 )2 |
B. ( ( )9( )9( )2× )2× |
C. ( ( )9( )9( )2 )2 |
D. ( ( )9( )9( )2 )2 |
甲乙两人分别独立参加某高校自主招生面试,若甲、乙能通过面试的概率都是 ,则面试结束后通过的人数X的数学期望是( )
,则面试结束后通过的人数X的数学期望是( )
A. |
B. |
C.1 | D. |
从1,2,3,4,5中选3个数,用ξ表示这3个数中最大的一个,则E(ξ)=( )
| A.3 | B.4.5 | C.5 | D.6 |