如图, 是以
是以 为直径的半圆
为直径的半圆 上异于
上异于 、
、 的点,矩形
的点,矩形 所在的平面垂直于半圆
所在的平面垂直于半圆 所在的平面,且
所在的平面,且 .
.
(1)求证: ;
;
(2)若异面直线 和
和 所成的角为
所成的角为 ,求平面
,求平面 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
已知集合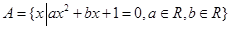 ,求
,求
(1)当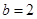 时,
时,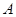 中至多只有一个元素,求
中至多只有一个元素,求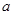 的取值范围;
的取值范围;
(2)当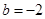 时,
时,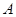 中至少有一个元素,求
中至少有一个元素,求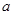 的取值范围;
的取值范围;
(3)当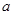 、
、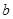 满足什么条件时,集合
满足什么条件时,集合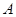 为非空集合。
为非空集合。
已知集合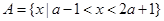 ,
,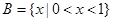 ,
,
(1)若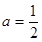 ,求
,求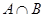 ;
;
(2)若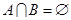 ,求实数a的取值范围.
,求实数a的取值范围.
已知在平面直角坐标系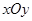 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为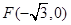 ,右顶点为
,右顶点为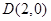 ,设点
,设点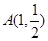 .
.
(Ⅰ)求该椭圆的标准方程;
(Ⅱ)过原点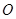 的直线交椭圆于点
的直线交椭圆于点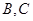 ,求
,求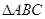 面积的最大值.
面积的最大值.
已知圆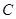 :
: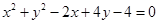 ,直线
,直线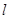 与圆
与圆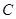 相交于
相交于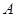 ,
,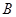 两点.
两点.
(Ⅰ)若直线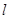 过点
过点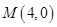 ,且
,且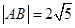 ,求直线
,求直线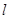 的方程;
的方程;
(Ⅱ)若直线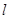 的斜率为
的斜率为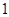 ,且以弦
,且以弦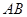 为直径的圆经过原点,求直线
为直径的圆经过原点,求直线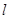 的方程.
的方程.
如图,在底面为平行四边形的四棱锥 中,
中, ,
, 平面
平面 ,且
,且 ,点
,点 是
是 的中点.
的中点.
(Ⅰ)求证: ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)若 ,求点
,求点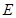 到平面
到平面 的距离.
的距离.