如图在四棱锥
中，底面
是菱形，
，平面
平面，
，
为
的中点，
是棱
上一点，且
.
（1）求证：
平面；
（2）证明：
∥平面
；
（3）求二面角
的度数.
（Ⅰ）已知
，求
（Ⅱ）已知
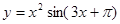，求
（本小题满分12分）
已知函数
．
（I）当
时，求函数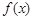
的单调区间；
（II）若函数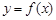
的图象在点
处的切线的倾斜角为45o，问：m在什么范围取值时，对于任意的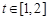
，函数
在区间
上总存在极值？
（本小题满分12分）已知双曲线
的两个焦点为
、
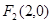点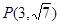
在双曲线C上.
(1)求双曲线C的方程；
(2)记O为坐标原点，过点Q (0,2)的直线l与双曲线C相交于不同的两点E、F，若△OEF的面积为
求直线l的方程.
（本小题满分12分）已知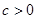
，设命题
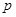:函数
为减函数，命题
：当
时，函数
恒成立；如果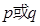
为真命题，
为假命题，求c的取值范围
（本小题满分12分）袋中有大小相同的红、黄两种颜色的球各1个，从中任取1只，有放回地抽取3次．求：
（Ⅰ）3只全是红球的概率；
（Ⅱ）3只颜色全相同的概率；
（Ⅲ）3只颜色不全相同的概率．