四棱锥 的底面是矩形,锥顶点在底面的射影是矩形对角线的交点,四棱锥及其三视图如下(AB平行于主视图投影平面)
的底面是矩形,锥顶点在底面的射影是矩形对角线的交点,四棱锥及其三视图如下(AB平行于主视图投影平面)
则四棱锥 的体积=( )
的体积=( )
| A.24 | B.18 | C. |
D.8 |
用反证法证明“a,b,c中至少有一个大于0”,下列假设正确的是( )
| A.假设a,b,c都小于0 |
| B.假设a,b,c都大于0 |
| C.假设a,b,c中都不大于0 |
| D.假设a,b,c中至多有一个大于0 |
分析法是从要证明的结论出发,逐步寻求使结论成立的( )
| A.充分条件 | B.必要条件 | C.充要条件 | D.等价条件 |
若P= +
+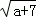 ,Q=
,Q= +
+ (a≥0),则P,Q的大小关系是( )
(a≥0),则P,Q的大小关系是( )
| A.P>Q | B.P=Q | C.P<Q | D.由a的取值确定 |
“因为指数函数y=ax是增函数,而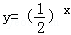 是指数函数,所以
是指数函数,所以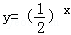 是增函数.”在以上三段论推理中( )
是增函数.”在以上三段论推理中( )
| A.大前提错误 |
| B.小前提错误 |
| C.推理形式错误 |
| D.大前提、小前提、推理形式错均正确 |
下列几种推理过程是演绎推理的是( )
| A.某校高三1班55人,2班54人,3班52人,由此得高三所有班级的人数超过50人 |
| B.由圆的周长C=πd推测球的表面积S=πd2 |
| C.两条直线平行,同旁内角互补,如果∠A与∠B是两条平行直线的同旁内角,则∠A+∠B=180° |
D.在数列{an}中,a1=1,an=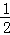 (an﹣1+ (an﹣1+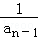 )(n≥2),由此归纳数列{an}的通项公式 )(n≥2),由此归纳数列{an}的通项公式 |