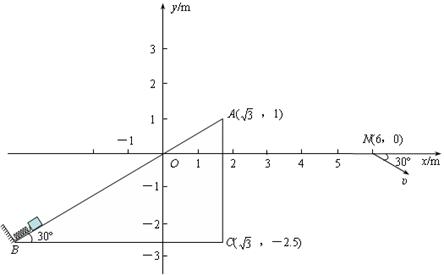
在竖直平面内存在如图所示的绝缘轨道，一质量为m=0.4kg、带电量为q=+0.4C的小滑块（可视为质点）在外力作用下压缩至离B点0.05m，此时弹性势能
=17.25J，弹簧一端固定在底端，与小滑块不相连，弹簧原长为2.05m，轨道与滑块间的动摩擦因数
．某时刻撤去外力，经过一段时间弹簧恢复至原长，再经过1.8s，同时施加电场和磁场，电场平行于纸面，且垂直x轴向上，场强E=10N/C；磁场方向垂直于纸面，且仅存在于第二、三象限内，最终滑块到达N（6m，0）点，方向与水平方向成30º斜向下．（答案可用π表示，
）
（1）求弹簧完全恢复瞬间，小滑块的速度；
（2）求弹簧原长恢复后1.8s时小滑块所在的位置；
（3）求小滑块在磁场中的运动的时间．
如图，厚度为D的玻璃砖与水平实验桌成45°角放置。红色激光束平行于水平桌面射到玻璃砖的表面，在桌面上得到两个较亮的光点
，测得
间的距离为L。求玻璃砖对该红色激光的折射率。
如图所示，A、B气缸的长度均为60cm，截面积均为40cm2，C是可在气缸内无摩擦滑动的、体积不计的活塞，D为阀门。整个装置均由导热材料制成。原来阀门关闭，A内有压强PA=2.4×105Pa的氧气．B内有压强PB=1．2×105Pa的氢气。阀门打开后，活塞C向右移动，最后达到平衡．求：
Ⅰ．活塞C移动的距离及平衡后B中气体的压强；
Ⅱ．活塞C移动过程中B中气体是吸热还是放热（简要说明理由）。
（假定氧气和氢气均视为理想气体，连接气缸的管道体积可忽略）
从阴极K发射的电子经电势差U0=4500V的阳极加速后，沿平行于板面的方向从中央射入两块长L1=10cm，间距d=4cm的平行金属板AB之后，在离金属板边缘L2=75cm处放置一个直径D=20cm的带有记录纸的圆筒（如图所示），整个装置放在真空内，电子发射的初速度不计。已知电子质量m=0.9×10-30 kg,电子电量e=1.6×10-19C,不考虑相对论效应。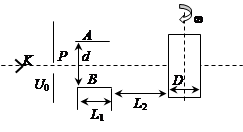
（1）若在两金属板上加上U1=1000V的直流电压（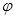
A>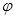B），为使电子沿入射方向做匀速直线运动，应加怎样的磁场？
（2）若在两金属板上加上U2=1000cos2πt（V）的交流电压，并使圆筒绕中心轴按图示方向以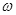
=4πrad/s的角速度匀速转动，确定电子在记录纸上的偏转位移随时间变化的关系式并定性画出1s钟内所记录的图形。（电子穿过AB的时间很短，可认为这段时间内板间电压不变）
一足够长水平浅色传送带以V0匀速运动，现将一可视为质点的小煤块轻放在其上方，已知煤块与传送带间的动摩擦因数为μ。经过一定时间后达到共同速度。令传送带突然停下，以后不再运动，到最后煤块也停下。已知重力加速度为g。求：（1）煤块第一次达到与传送带相对静止所用的时间；（2）煤块在传送带上划出的痕迹长度。
示波器的示意图如图所示，金属丝发射出来的电子被加速后从金属板的小孔穿出，进入偏转电场．电子在穿出偏转电场后沿直线前进，最后打在荧光屏上．设加速电压U1＝1640V，偏转极板长l＝4cm，偏转板间距d＝1 cm，当电子加速后从两偏转极板的中央沿板平行方向进入偏转电场．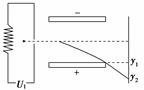
(1)偏转电压为多大时，电子束打在荧光屏上偏转距离最大？
(2)如果偏转板右端到荧光屏的距离L＝20 cm，则电子束最大偏转距离为多少？