如图所示,某旅游景点有一座风景秀丽的山峰,山上有一条笔直的山路BC和一条索道AC,小王和小李打算不坐索道,而是花2个小时的时间进行徒步攀登.已知 ,
, ,
, (千米),
(千米), (千米).假设小王和小李徒步攀登的速度为每小时1200米,请问:两位登山爱好者能否在2个小时内徒步登上山峰.
(千米).假设小王和小李徒步攀登的速度为每小时1200米,请问:两位登山爱好者能否在2个小时内徒步登上山峰.
(即从B点出发到达C点)
(本小题满分12分)
已知 是首项为
是首项为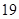 ,公差为
,公差为 的等差数列.
的等差数列.
(1)求通项 ;
;
(2)设 是首项为
是首项为 ,公比为
,公比为 的等比数列,求数列
的等比数列,求数列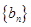 的通项公式及其前
的通项公式及其前 项和
项和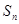 .
.
本小题满分10分)
在△ABC中,A、B为锐角,角A、B、C所对的边分别为 、
、 、
、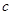 ,且
,且 ,
, 。
。
(1)求角C的值;
(2)若a-b=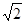 -1,求
-1,求 、
、 、
、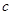 的值。
的值。
.已知数列{an}满足a1=1,a2=r(r>0),数列{bn}是公比为q的等比数列(q>0),bn=anan+1,cn=a2n-1+a2n,求cn。
陈老师购买安居工程集资房7m2,单价为1000/ m2,一次性国家财政补贴28800元,学校补贴14400元,余款由个人负担,房地产开发公司对教师实行分期付款,即各期所付的款以及各期所付的款到最后一次付款时所生的利息合计,应等于个人负担的购房余款的现价以及这个余款现价到最后一次付款时所生利息之和,每期为一年,等额付款,签订购房合同后一年付款一次,再过一年又付款一次等等,若付10次,10年后付清。如果按年利率的7.5%每年复利一次计算(即本年利息计入次年的本金生息),那么每年应付款多少元?(参考数据:1.0759 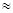 1.921,1.07510
1.921,1.07510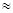 2.065,1.07511
2.065,1.07511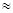 2.221)
2.221)
某企业年初有资金1000万元,如果该企业经过生产经营,每年资金增长率为50%,但每年年底都要扣除消费基金x万元,余下资金投入再生产,为实现经过五年,资金达到2000万元(扣除消费基金后),那么每年扣除的消费资金应是多少万元(精确到万元)。