已知甲同学手中藏有三张分别标有数字 ,
,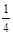 ,1的卡片,乙同学手中藏有三张分别标有数字1,3,2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片.
,1的卡片,乙同学手中藏有三张分别标有数字1,3,2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片.
(1)请你用树形图或列表法列出所有可能的结果;
(2)求抽出的两张卡片数字积恰好为1的概率.
.在△ABC中,AB=CB,∠ABC=90º,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=35º,求∠ACF度数.
.如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.试猜想线段BC和EF的数量及位置关系,并证明你的猜想
如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9.
(1)求DC和AB的长;
(2)证明:∠ACB=90°.
如图:已知∠AOB和C、D两点,求作一点P,使PC=PD,且P到∠AOB两边的距离相等.(保留作图痕迹,不写作法)
如图,E、F是四边形ABCD的对角线BD上的两点, AE∥CF,AE=CF,BE=DF.
求证: ΔADE≌ΔCBF.