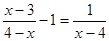综合实践课上，小明所在小组要测量护城河的宽度．如图所示是护城河的一段，两岸AB∥CD，河岸AB上有一排大树，相邻两棵大树之间的距离均为10米.小明先用测角仪在河岸CD的M处测得∠α=36°，然后沿河岸走50米到达N点，测得∠β=72°．请你根据这些数据帮小明他们算出河宽FR（结果保留两位有效数字）.
（参考数据：sin36°≈0.59，cos36°≈0.81，tan36°≈0.73，sin72°≈0.95，cos72°≈0.31，tan72°≈3.08） 
如图，△ABC中，∠B=60，∠ACB=75，点D是BC边上一动点，以AD为直径作⊙O，分别交AB、AC于E、F，若弦EF的最小值为1，则AB的长为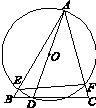
A． |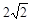
B． |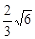
C．1.5 | D． |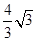
如图1，在Rt△ABC中，∠C＝90°，BC＝8厘米，点D在AC上，CD＝3厘米．点P、Q分别由A、C两点同时出发，点P沿AC方向向点C匀速移动，速度为每秒k厘米，行完AC全程用时8秒；点Q沿CB方向向点B匀速移动，速度为每秒1厘米．设运动的时间为x秒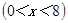
，△DCQ的面积为y1平方厘米，△PCQ的面积为y2平方厘米．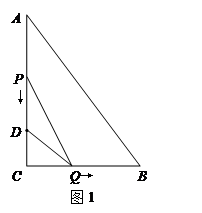
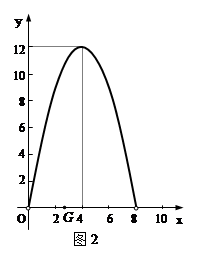
（1）求y1与x的函数关系，并在图2中画出y1的图象；
（2）如图2，y2的图象是抛物线的一部分，其顶点坐标是（4，12），求点P的速度及AC的长；
（3）在图2中，点G是x轴正半轴上一点（0＜OG＜6），过G作EF垂直于x轴，分别交y1、y2于点E、F．
①说出线段EF的长在图1中所表示的实际意义；
②当0＜x＜６时，求线段EF长的最大值．
如图，在△ABC中，点O是AC边上的一动点，过点O作直线MN//BC，MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F。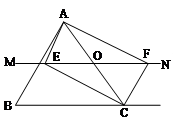
（1）求证：EO=FO；
（2）当点O运动到何处时，四边形AECF是矩形？证明你的结论；
（3）说明，当点O运动到何处时，且△ABC具备什么条件时，四边形AECF是正方形（不证明）
某商场将进价40元一个的某种商品按50元一个售出时，能卖出500个，已知这种商品每个涨价一元，销量减少10个，为赚得最大利润，售价定为多少？最大利润是多少？
解方程：