为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时.为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:

(1)在这次调查中共调查了多少名学生?
(2)求户外活动时间为1.5小时的人数,并补充频数分布直方图;
(3)求表示户外活动时间 1小时的扇形圆心角的度数;
(4)本次调查中学生参加户外活动的平均时间是否符合要求?户外活动时间的众数和中位数是多少?
(本题满分12分)在 中,
中,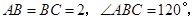 将
将 绕点
绕点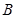 顺时针旋转角
顺时针旋转角
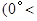

 得
得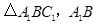 交
交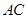 于点
于点 ,
, 分别交
分别交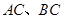 于
于 两点.
两点.(1)如图1,观察并猜想,在旋转过程中,线段
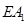 与
与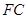 有怎样的数量关系?并证明你的结论;
有怎样的数量关系?并证明你的结论;(2)如图2,当

 时,试判断四边形
时,试判断四边形 的形状,并说明理由;
的形状,并说明理由;(3)在(2)的情况下,求
 的长.
的长.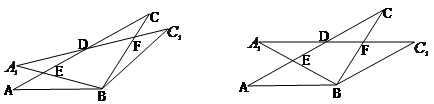
(本题满分12分)有一批图形计算器,原售价 为每台800元,在甲、乙两家公司销售.甲公司用如下方法促销:买一台单价为780元,买两台每台都为760元.依此类推,即每多买一台则所买各台单价均再减20元,但最低不能低于每台440元;乙公司一律按原售价的75%促销.某单位需购买一批图形计算器:
为每台800元,在甲、乙两家公司销售.甲公司用如下方法促销:买一台单价为780元,买两台每台都为760元.依此类推,即每多买一台则所买各台单价均再减20元,但最低不能低于每台440元;乙公司一律按原售价的75%促销.某单位需购买一批图形计算器:(1)若此单位需购买6台图形计算器,应去哪家公司购买花费较少?
(2)若此单位恰好花费7 500元,在同一家公司购买了一定数量的图形计算器,请问是在哪家公司购买的,数量是多少?
如图,在Rt△ABC中,∠ACB=90°,AC=6㎝,BC=8㎝,P为BC的中点.动点Q从点P出发,沿射线PC方向以2㎝/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.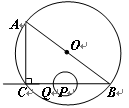
⑴求 AB的长;
⑵已知⊙O为△ABC的外接圆,若⊙P与
 ⊙O相切,求t的值.
⊙O相切,求t的值.
(本题满分8分)如图,AD是⊙O的弦,AB经过圆心O,交⊙O于点C.∠DAB=∠B=30°.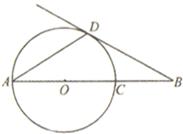
(1)直线BD是否与⊙O相切?为什么?
(2)连接CD,若CD=5,求AB的长.
(本题满分8分)已知一元二次方程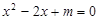 .
.(1)若方程有两个实数根,求m的范围;
(2)若方程的两个实数根为x1,x2,且
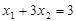 ,
, 求m的值.
求m的值.