如图1,已知正方形ABCD的边长为1,点E在边BC上,若∠AEF=90°,且EF交正方形外角的平分线CF于点F.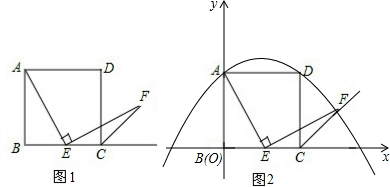
(1)图1中若点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);
(2)如图2,若点E在线段BC上滑动(不与点B,C重合).
①AE=EF是否总成立?请给出证明;
②在如图2的直角坐标系中,当点E滑动到某处时,点F恰好落在抛物线y=-x2+x+1上,求此时点F的坐标.
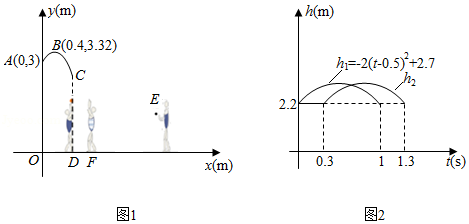
在篮球比赛中,东东投出的球在点 处反弹,反弹后球运动的路线为抛物线的一部分(如图1所示建立直角坐标系),抛物线顶点为点 .
(1)求该抛物线的函数表达式.
(2)当球运动到点 时被东东抢到, 轴于点 , .
①求 的长.
②东东抢到球后,因遭对方防守无法投篮,他在点 处垂直起跳传球,想将球沿直线快速传给队友华华,目标为华华的接球点 .东东起跳后所持球离地面高度 (传球前)与东东起跳后时间 满足函数关系式 ;小戴在点 处拦截,他比东东晚 垂直起跳,其拦截高度 与东东起跳后时间 的函数关系如图2所示(其中两条抛物线的形状相同).东东的直线传球能否越过小戴的拦截传到点 ?若能,东东应在起跳后什么时间范围内传球?若不能,请说明理由(直线传球过程中球运动时间忽略不计).
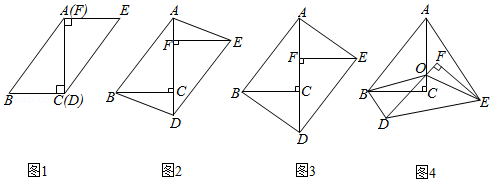
在一次数学研究性学习中,小兵将两个全等的直角三角形纸片 和 拼在一起,使点 与点 重合,点 与点 重合(如图 ,其中 , , ,并进行如下研究活动.
活动一:将图1中的纸片 沿 方向平移,连结 , (如图 ,当点 与点 重合时停止平移.
[思考]图2中的四边形 是平行四边形吗?请说明理由.
[发现]当纸片 平移到某一位置时,小兵发现四边形 为矩形(如图 .求 的长.
活动二:在图3中,取 的中点 ,再将纸片 绕点 顺时针方向旋转 度 ,连结 , (如图 .
[探究]当 平分 时,探究 与 的数量关系,并说明理由.
为了测量一条两岸平行的河流宽度,三个数学研究小组设计了不同的方案,他们在河南岸的点 处测得河北岸的树 恰好在 的正北方向.测量方案与数据如下表:
|
课题 |
测量河流宽度 |
||
|
测量工具 |
测量角度的仪器,皮尺等 |
||
|
测量小组 |
第一小组 |
第二小组 |
第三小组 |
|
测量方案示意图 |
|
|
|
|
说明 |
点 , 在点 的正东方向 |
点 , 在点 的正东方向 |
点 在点 的正东方向,点 在点 的正西方向. |
|
测量数据 |
, , . |
, , . |
, , . |
(1)哪个小组的数据无法计算出河宽?
(2)请选择其中一个方案及其数据求出河宽(精确到 .(参考数据: , , ,

小吴家准备购买一台电视机,小吴将收集到的某地区 、 、 三种品牌电视机销售情况的有关数据统计如下:
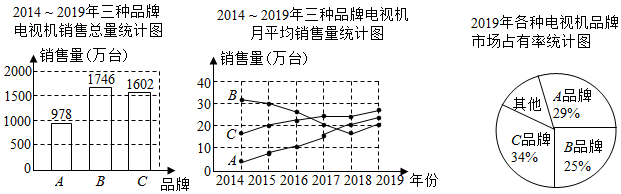
根据上述三个统计图,请答案:
(1) 年三种品牌电视机销售总量最多的是 品牌,月平均销售量最稳定的是 品牌.
(2)2019年其他品牌的电视机年销售总量是多少万台?
(3)货比三家后,你建议小吴家购买哪种品牌的电视机?说说你的理由.
经过实验获得两个变量 , 的一组对应值如下表.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
6 |
2.9 |
2 |
1.5 |
1.2 |
1 |
(1)请画出相应函数的图象,并求出函数表达式.
(2)点 , , , 在此函数图象上.若 ,则 , 有怎样的大小关系?请说明理由.
