(1)开普勒从1609年~1619年发表了著名的开普勒行星运动三定律,其中第一定律为:所有的行星分别在大小不同的椭圆轨道上围绕太阳运动,太阳在这个椭圆的一个焦点上。第三定律:所有行星的椭圆轨道的半长轴的三次方跟公转周期的平方的比值都相等.实践证明,开普勒三定律也适用于其他中心天体的卫星运动。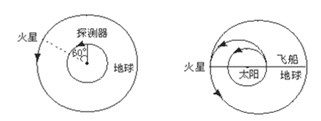
(2)从地球表面向火星发射火星探测器.设地球和火星都在同一平面上绕太阳做圆周运动,火星轨道半径Rm为地球轨道半径R0的1.5倍,简单而又比较节省能量的发射过程可分为两步进行:第一步,在地球表面用火箭对探测器进行加速,使之获得足够动能,从而脱离地球引力作用成为一个沿地球轨道运动的人造行星。第二步是在适当时刻点燃与探测器连在一起的火箭发动机,在短时间内对探测器沿原方向加速,使其速度数值增加到适当值,从而使得探测器沿着一个与地球轨道及火星轨道分别在长轴两端相切的半个椭圆轨道正好射到火星上.当探测器脱离地球并沿地球公转轨道稳定运行后,在某年3月1日零时测得探测器与火星之间的角距离为60°,如图所示,问应在何年何月何日点燃探测器上的火箭发动机方能使探测器恰好落在火星表面?(时间计算仅需精确到日),已知地球半径为: ;
; ;
;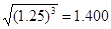
如图所示,水平地面上放置一个质量为m的物体,在与水平方向成θ角、斜向右上方的拉力F的作用下沿水平地面运动。物体与地面间的动摩擦因数为μ,重力加速度为g。求: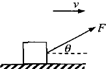
(1)若物体在拉力F的作用下能始终沿水平面向右运动,拉力F的大小范围;
(2)已知m=10 kg、μ=0.5,g=10 m/s2,若物体以恒定加速度a=5 m/s2向右做匀加速直线运动,维持这一加速度的拉力F的最小值。
如图,光滑水平面上有三个物块A、B和C,它们具有相同的质量,且位于同一直线上。开始时,三个物块均静止,先让A以一定速度与B碰撞,碰后它们粘在一起,然后又一起与C碰撞并粘在一起,求前后两次碰撞中系统损失的动能之比。 
如图所示,一长为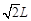 的木板,倾斜放置,倾角为45°,现有一弹性小球,从与木板上端等高的某处自由释放,小球落到木板上反弹时,速度大小不变,碰撞前后,速度方向与木板的夹角相等,欲使小球一次碰撞后恰好落到木板下端,则小球释放点距木板上端的水平距离为___________。
的木板,倾斜放置,倾角为45°,现有一弹性小球,从与木板上端等高的某处自由释放,小球落到木板上反弹时,速度大小不变,碰撞前后,速度方向与木板的夹角相等,欲使小球一次碰撞后恰好落到木板下端,则小球释放点距木板上端的水平距离为___________。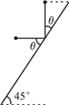
(1)在匀强磁场中,有一个原来静止的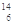 C原子核,它放出的粒子与反冲核的径迹是两个相内切的圆,圆的直径之比为7:1,那么碳14的衰变方程应为()
C原子核,它放出的粒子与反冲核的径迹是两个相内切的圆,圆的直径之比为7:1,那么碳14的衰变方程应为()
A.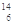 C → C → 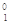 e+ e+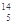 B B |
B.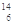 C → C → 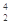 He+ He+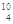 Be Be |
C.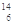 C → C → 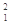 H+ H+ B B |
D.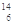 C → C → 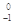 e+ e+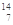 N N |
(2)如图所示,光滑水平面上有带有1/4光滑圆弧轨道的滑块,其质量为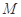 ,一质量为
,一质量为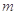 的小球,以速度
的小球,以速度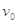 沿平面滑上轨道,并从轨道上端飞出,问小球上升到离水平面多高处?
沿平面滑上轨道,并从轨道上端飞出,问小球上升到离水平面多高处?
(I)关于一定量的气体,下列说法正确的是
| A.气体的体积指的是该气体的分子所能到达的空间的体积,而不是该气体所有分子体积之和 |
| B.只要能减弱气体分子热运动的剧烈程度,气体的温度就可以降低 |
| C.在完全失重的情况下,气体对容器壁的压强为零 |
| D.气体从外界吸收热量,其内能一定增加 |
E.气体在等压膨胀过程中温度一定升高。
(2)如图,一上端开口、下端封闭的细长玻璃管竖直放置。玻璃管的下部封有长ll=25.0cm的空气柱,中间有一段长为l2=25.0cm的水银柱,上部空气柱的长度l3=40.0cm。已知大气压强为P0=75.0cmHg。现将一活塞(图中未画出)从玻璃管开口处缓缓往下推,使管下部空气柱长度变为l'1=20.0cm。假设活塞下推过程中没有漏气,求活塞下推的距离。