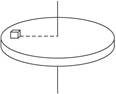
如图甲所示,水平加速电场的加速电压为U0,在它的右侧有由水平正对放置的平行金属板a、b构成的偏转电场,已知偏转电场的板长L="0.10" m,板间距离d=5.0×10-2m,两板间接有如图15乙所示的随时间变化的电压U,且a板电势高于b板电势。在金属板右侧存在有界的匀强磁场,磁场的左边界为与金属板右侧重合的竖直平面MN,MN右侧的磁场范围足够大,磁感应强度B=5.0×10-3T,方向与偏转电场正交向里(垂直纸面向里)。质量和电荷量都相同的带正电的粒子从静止开始经过电压U0=50V的加速电场后,连续沿两金属板间的中线OO′方向射入偏转电场中,中线OO′与磁场边界MN垂直。已知带电粒子的比荷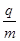 =1.0×108C/kg,不计粒子所受的重力和粒子间的相互作用力,忽略偏转电场两板间电场的边缘效应,在每个粒子通过偏转电场区域的极短时间内,偏转电场可视作恒定不变。
=1.0×108C/kg,不计粒子所受的重力和粒子间的相互作用力,忽略偏转电场两板间电场的边缘效应,在每个粒子通过偏转电场区域的极短时间内,偏转电场可视作恒定不变。
(1)求t=0时刻射入偏转电场的粒子在磁场边界上的入射点和出射点间的距离;
(2)求粒子进入磁场时的最大速度;
(3)对于所有进入磁场中的粒子,如果要增大粒子在磁场边界上的入射点和出射点间的距离,应该采取哪些措施?试从理论上推理说明。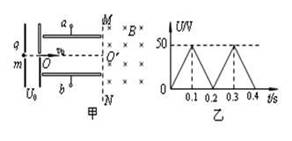
天文观测指出,太阳在一个绕银河系中心的圆形轨道上运行,这个轨道的半径约为3万光年(2.7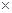 1020m),绕行周期约为2亿年,太阳做这种运动所受的力是那些位于轨道内侧的大量星体的引力。求;
1020m),绕行周期约为2亿年,太阳做这种运动所受的力是那些位于轨道内侧的大量星体的引力。求;
(1)如果把这些星体看成集中在轨道的中心,那么这些星体的总质量为多少?
(2)这些星体的总质量相当于多少个太阳的质量?(太阳的质量约为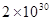
 kg)
kg)
在天体运动中,把两颗相距较近的恒星称为双星,它们各自以对方给予的万有引力为向心力(不计其它星球对它们的影响)。已知A、B两恒星质量分别为M和m,两恒星相距为L,两恒星分别绕共同的圆心做圆周运动,如图,求两恒星的轨道半径和角速度大小。
用火箭把宇航员送到月球上,如果已知月球的半径,他用一个弹簧秤和一个已知质量的砝码,能否测出月球的质量?应该怎样测定?
已知太阳光从太阳射到地球需要约500s,地球绕太阳公转周期约为 s,地球的质量约为
s,地球的质量约为 kg。试求太阳对地球的引力为多大?(结果保留一位有效数字)
kg。试求太阳对地球的引力为多大?(结果保留一位有效数字)
如图所示,一木块放于水平转盘上,与转轴的距离为r,若木块与盘面间的最大静摩擦力是木块重力的μ倍,为使木块不与转盘发生相对移动,转盘转动的角速度的最大值是________________.