在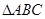 中,若
中,若 ,则
,则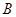 等于( )
等于( )
A.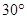 |
B. |
C. |
D.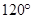 |
已知地球的半径为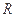 ,球面上
,球面上 两点都在北纬45°圈上,它们的球面距离为
两点都在北纬45°圈上,它们的球面距离为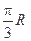 ,
,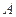 点在东经30°上,则
点在东经30°上,则 两点所在其纬线圈上所对应的劣弧的长度为()
两点所在其纬线圈上所对应的劣弧的长度为()
A. |
B.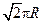 |
C.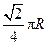 |
D.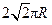 |
 、
、 是半径为
是半径为 的球
的球 的球面上两点,它们的球面距离为
的球面上两点,它们的球面距离为 ,求过
,求过 、
、 的平面中,与球心的最大距离是()
的平面中,与球心的最大距离是()
A.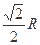 |
B.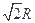 |
C.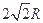 |
D.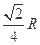 |
已知A,B两地都位于北纬45°,又分别位于东经30°和60°,设地球半径为R,则A,B的球面距离约为 ( )
A.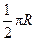 |
B. |
C. |
D.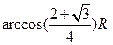 |
设地球半径为R,则东经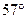 线上,纬度分别为北纬
线上,纬度分别为北纬 和
和 的两地A,B的球面距离为( )
的两地A,B的球面距离为( )
A.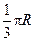 |
B. |
C.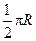 |
D. |
平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为 ,则此球的体积为( )
,则此球的体积为( )
A.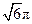 |
B. |
C.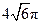 |
D.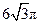 |