安徽理)(设椭圆 的焦点在
的焦点在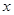 轴上
轴上
(1)若椭圆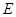 的焦距为1,求椭圆
的焦距为1,求椭圆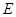 的方程;
的方程;
(2)设 分别是椭圆的左、右焦点,
分别是椭圆的左、右焦点,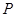 为椭圆
为椭圆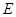 上第一象限内的点,直线
上第一象限内的点,直线 交
交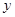 轴与点
轴与点 ,并且
,并且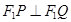 ,证明:当
,证明:当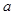 变化时,点
变化时,点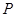 在某定直线上。
在某定直线上。
某商场销售某种商品的经验表明,该商品每日的销售量 (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式 其中
其中 为常数.己知销售价格为5元/千克时,每日可售出该商品11千克.
为常数.己知销售价格为5元/千克时,每日可售出该商品11千克.
(1)求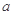 的值;
的值;
(2)若该商品的成本为3元/千克,试确定销售价格 的值,使商场每日销售该商品所获得利润最大.
的值,使商场每日销售该商品所获得利润最大.
已知函数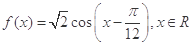 .
.
(1)求 的值;
的值;
(2)若 ,求
,求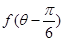 .
.
已知函数 .
.
(1)求 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;
(2)若 在区间
在区间 上的最大值与最小值的和为
上的最大值与最小值的和为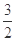 ,求
,求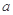 的值.
的值.
在直角坐标平面内,以坐标原点 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点 的极坐标为
的极坐标为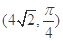 ,曲线
,曲线 的参数方程为
的参数方程为 (
( 为参数).
为参数).
(1)求直线 的直角坐标方程;
的直角坐标方程;
(2)求点 到曲线
到曲线 上的点的距离的最小值.
上的点的距离的最小值.
记函数 的定义域为集合
的定义域为集合 ,函数
,函数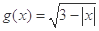 的定义域为集合
的定义域为集合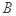 .
.
(1)求
 ;
;
(2)若 ,且
,且 ,求实数
,求实数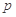 的取值范围.
的取值范围.