某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横的交叉点记忆三角形的顶点)处都种了一株相同品种的作物。根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如下表所示:
| X |
1 |
2 |
3 |
4 |
| Y |
51 |
48 |
45 |
42 |
这里,两株作物“相近”是指它们之间的直线距离不超过1米。

(1)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率;
(2)从所种作物中随机选取一株,求它的年收获量的分布列与数学期望。
设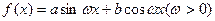 的周期
的周期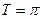 ,最大值
,最大值 ,
,
(1)求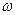 、
、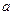 、
、 的值;
的值;
(2) .
.
实数 满足
满足 求
求 的值.
的值.
已知函数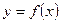 的图象关于直线
的图象关于直线 对称,当
对称,当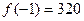 ,
,
且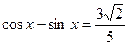 时,试求
时,试求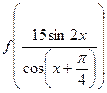 的值.
的值.
如图,在锐角△ABC中,AB<AC,AD是边BC上的高,P是线段AD内一点。过P作PE⊥AC,垂足为E,做PF⊥AB,垂足为F。O1、O2分别是△BDF、△CDE的外心。求证:O1、O2、E、F四点共圆的充要条件为P是△ABC的垂心。
设函数f(x)对所有的实数x都满足f(x+2π)=f(x),求证:存在4个函数fi(x)(i=1,2,3,4)满足:(1)对i=1,2,3,4,fi(x)是偶函数,且对任意的实数x,有fi(x+π)=fi(x);(2)对任意的实数x,有f(x)=f1(x)+f2(x)cosx+f3(x)sinx+f4(x)sin2x。