滑板运动是一项陆地上的“冲浪运动”,具有很强的观赏性与趣味性。下坡式滑行轨道可H简化为如下模型:如图所示,abcdf为同一竖直平面内的滑行轨道,其中ab、df两段均为倾角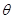 =37o的斜直粗糙轨道,bc为一段半径为R=5m的光滑圆弧,圆弧与ab相切于磊点,圆弧圆心O在c点的正上方。已知ab之间高度差H1=5rn,cd之间高度差H2=2.25m,运动员连同滑板的总质量m=60kg。运动员从a点由静止开始下滑后从C点水平飞出,落在轨道上的e点,经短暂的缓冲动作后沿斜面方向下滑。de之间的高度差H3="9" m,运动员连同滑板可视为质点,忽略空气阻力,取g =10m/s2,sin37o=0.6,cos37o=0.8 。求:
=37o的斜直粗糙轨道,bc为一段半径为R=5m的光滑圆弧,圆弧与ab相切于磊点,圆弧圆心O在c点的正上方。已知ab之间高度差H1=5rn,cd之间高度差H2=2.25m,运动员连同滑板的总质量m=60kg。运动员从a点由静止开始下滑后从C点水平飞出,落在轨道上的e点,经短暂的缓冲动作后沿斜面方向下滑。de之间的高度差H3="9" m,运动员连同滑板可视为质点,忽略空气阻力,取g =10m/s2,sin37o=0.6,cos37o=0.8 。求:
(1)运动员刚运动到c点时的速度大小;
(2)运动员(连同滑板)刚运动到c点时对轨道的压力;
(3)运动员(连同滑板)在由a点运动到b点过程中阻力对它做的功。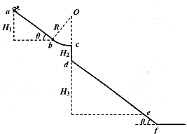
下图是一个设计“过山车”的试验装置的原理示意图。斜面AB与竖直面内的圆形轨道在B点平滑连接。斜面AB和圆形轨道都是光滑的。圆形轨道半径为R。一个质量为m的小车(可视为质点)在A点由静止释放沿斜面滑下,小车恰能通过圆形轨道的最高点C。已知重力加速度为g。 
求:(1)A点距水平面的高度h;
(2)在B点轨道对小车的支持力的大小。
水上滑板是一项非常刺激的运动,研究表明,在进行水上滑板运动时,水对滑板的作用力Fx垂直于板面,大小为kv2,其中v为滑板速率(水可视为静止)。某次运动中,在水平牵引力作用下,当滑板和水面的夹角=" 37°" 时(题图),滑板做匀速直线运动,相应的k =" 54" kg/m,人和滑板的总质量为108 kg,试求(重力加速度g取10 m/s2,sin 37°取 ,忽略空气阻力):
,忽略空气阻力):
(1)水平牵引力的大小;
(2)滑板的速率;
(3)水平牵引力的功率。
把一个质量为1 kg的物体放在水平面上,用8 N的水平拉力使物体从静止开始运动,物体与水平面的动摩擦因数为0.2,物体运动2 s时撤掉拉力。(g取10 m/s2)
求:(1)2 s末物块的动能。
(2)2 s后物块在水平面上还能向前滑行的最大距离。
如图所示,质量为m=4kg的物体静止在水平面上,在外力F=25N作用下开始运动,已知F与水平方向夹角θ=37˚,物体位移为5m时,物体的速度变为5 m/s 。求:(取g=10m/s2)(sin370="0.6" , cos370=0.8)
(1) 此过程中,物体克服摩擦力所做的功;
(2) 物体与水平面间的动摩擦因数μ
土星周围有许多大小不等的岩石颗粒,其绕土星的运动可视为匀速圆周运动。其中两个岩石颗粒A和B与土星中心距离分别为RA和RB。忽略所有岩石颗粒间的相互作用。
(1)求岩石颗粒A和B的线速度之比
(2)求岩石颗粒A和B的周期之比