有一个小圆环瓷片最高能从h=0.18m高处静止释放后直接撞击地面而不被摔坏。现让该小圆环瓷片恰好套在一圆柱体上端且可沿圆柱体下滑，瓷片与圆柱体之间的摩擦力是瓷片重力的4.5倍，如图所示。若将该装置从距地面H=4.5m高处从静止开始下落，瓷片落地恰好没摔坏。已知圆柱体与瓷片所受的空气阻力都为自身重力的0.1倍，圆柱体碰地后速度立即变为零且保持竖直方向。（g=10m/s2）
⑴瓷片直接撞击地面而不被摔坏时，瓷片着地时的最大速度为多少？
⑵瓷片随圆柱体从静止到落地，下落总时间为多少？
水平面上质量为l0kg的木块，在25N水平力作用下运动，若木块与水平面间的动摩擦因数
0．2，如图所示，求：木块所受合力的大小和方向．（
）
多数情况下，物体间的最大静摩擦力大于滑动摩擦力，最大静摩擦力的大小与物体间的正压力有关，正压力越大，最大静摩擦力越大，它们间的定量关系是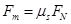
，其中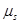
是静摩擦因数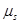，的大小与接触物体间的材质及接触面粗糙程度有关。在平整的雪地上拉一个25kg的雪橇，静摩擦因数和滑动摩擦因数分别为0.30和0.10。（g取10N/kg）试求：
（1）雪橇多重？
（2）当站上65kg的人后，用至少多大的水平拉力才能使雪橇滑动起来？
（3）若让站在雪橇上的人保持匀速运动，要用多大的水平拉力？
质量为2kg的物体，静止在水平地面上，如图所示，物体与水平地面间的动摩擦因数
，物体受到水平向右的拉力
.
（1）当拉力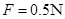
时，物体静止不动，物体受到的摩擦力为多大？
（2）当拉力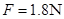
时，物体静止不动，物体受到的摩擦力为多大？
（3）当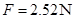
时，物体恰好开始运动，物体受到的摩擦力为多大？
一根弹簧在弹性限度内，对其施加30N的拉力时其长20cm，对其施加30N的压力时，其长14cm，则该弹簧的自然长度是多少？其劲度系数是多少？
如图所示为粮食仓库中常用的皮带传输装置示意图，它由两台皮带传送机组成，一台水平传送，A、B两端相距
；另一台倾斜传送，传送带与地面间的倾角
，C、D两端相距
，B、C相距很近。水平传送带以
沿顺时针方向转动。现将质量为
的一袋大米无初速度的放在A端，它随传送带到达B点后，速度大小不变的传到倾斜传送带的C端。米袋与两传送带之间的动摩擦因素均为
，取
（1）若倾斜传送带CD不转动，则米袋沿传送带CD所能上滑的最大距离是多少？
（2）若倾斜传送带CD以
的速率沿顺时针方向转动，则米袋从C端运动到D端的时间为多少？