如图所示,ABCD为固定在竖直平面内的轨道,AB段光滑水平,BC段为光滑圆弧,对应的圆心角θ = 370,半径r = 2.5m,CD段平直倾斜且粗糙,各段轨道均平滑连接,倾斜轨道所在区域有场强大小为E = 2×105N/C、方向垂直于斜轨向下的匀强电场。质量m = 5×10-2kg、电荷量q =+1×10-6C的小物体(视为质点)被弹簧枪发射后,沿水平轨道向左滑行,在C点以速度v0=3m/s冲上斜轨。以小物体通过C点时为计时起点,0.1s以后,场强大小不变,方向反向。已知斜轨与小物体间的动摩擦因数μ=0.25。设小物体的电荷量保持不变,取g=10m/s2,sin370=0.6,cos370=0.8。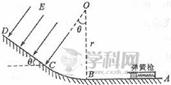
(1)求弹簧枪对小物体所做的功;
(2)在斜轨上小物体能到达的最高点为P,求CP的长度。
如图所示,质量为m、边长为L的正方形线框,从有界的匀强磁场上方由静止自由下落,线框电阻为R,匀强磁场的高度为H,(L<H),磁感应强度为B,线框下落过程中ab边与磁场边界平行且保持水平。已知ab边刚进入磁场时和ab边刚穿出磁场时线框都做减速运动,加速度大小都为 .求:
.求:
(1)ab边刚进入磁场时和ab边刚出磁场时的速度大小;
(2)cd边刚进入磁场时,线框的速度大小;
(3)线框进入磁场的过程中,产生的热量.
起重机将质量为m=5x103 kg的物体由静止竖直吊起,起吊过程中做匀加速直线运动a=0.2m/s2,当起重机输出功率达到其允许的最大时,保持该功率直到重物以Vm=1.02m/s做匀速运动,g="10" m/s2,不计其他额外功
(1)、起重机允许输出的最大功率
(2)、重物做匀加速运动所经历的时间和起重机在第2秒末的输出功率
如图,质量为m的小铁块A以水平速度V0冲上质量为M,长度为l,置于光滑水平面C上的木板B,正好不从木块板上掉下,已知A、B间的动摩擦因数为u,此时长木板对地位移为S,求这一过程中: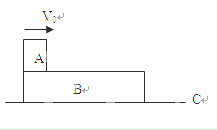
(1)、木板增加的动能
(2)、小铁块减少的动能
(3)、系统机械能的减少量
(4)、系统产生的热量
A物体做匀速直线运动,速度是1m/s. A出发后5s,B物体从同一地点由静止开始出发做匀加速直线运动,加速度是0.4m/s2,且A、B运动方向相同,求:
(1)B出发几秒后能追上A?
(2)A、B相遇前它们之间的最大距离是多少?
甲车以10m/s的速度匀速运动,在某时刻经过乙车身边,此时乙车的速度为2m/s,加速度为0.2m/s2,若甲乙两车运动方向相同,公路是平直的,问:
(1)当乙车速度多大时,乙车落后于甲车的距离最大?这个距离是多少?
(2)当乙车的速度多大时,乙车追上甲车?乙车追上甲车所需的时间是多少?