2014年索契冬奥会冰壶比赛在北京时间2月10日-21日进行。冰壶比赛是在水平冰面上进行的体育项目，比赛场地示意如图．比赛时运动员在投掷线AB处让冰壶以v0=2m/s的初速度向圆垒圆心O点滑出，已知圆垒圆心O到AB线的距离为30m，冰壶与冰面间的动摩擦因数为µ1=0.008(g取10m/s2)．问：
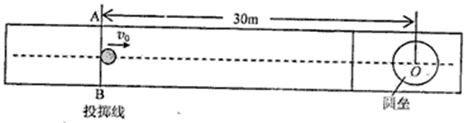
(1)如果在圆垒圆心O有对方的冰壶，则能否与对方冰壶相撞?请通过计算说明理由．
(2)如果在圆垒圆心O有对方的冰壶，为了确保将对方冰壶撞开，运动员可以用毛刷擦冰壶运行前方的冰面，使冰壶与冰面间的动摩擦因数减小，若用毛刷擦冰面后动摩擦因数减少至, µ2=0.004，则运动员用毛刷擦冰面的长度应大于多少米?
如图所示，半径R = 0.8m的光滑绝缘导轨固定于竖直平面内，加上某一方向的匀强电场时，带正电的小球沿轨道内侧做圆周运动．圆心O与A点的连线与竖直成一角度θ，在A点时小球对轨道的压力N = 120N，此时小球的动能最大。若小球的最大动能比最小动能多32J，且小球能够到达轨道上的任意一点（不计空气阻力）。则：
（1）小球的最小动能是多少？
（2）小球受到重力和电场力的合力是多少？
（3）现小球在动能最小的位置突然撤去轨道，并保持其他量都不变，若小球在0.04s后的动能与它在A点时的动能相等，求小球的质量。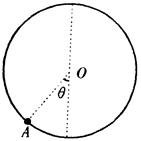
如图所示电路中，甲、乙两个毫安表的内阻均为6Ω，R3＝12Ω，S断开时，AB之间电阻为3Ω,S闭合时，甲、乙两个毫安表的示数之比为1:2，求R1、R2的阻值各为多少？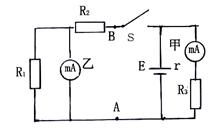
两平行金属板间所加电压随时间变化的规律如图所示，大量质量为m、带电量为e的电子由静止开始经电压为U0的电场加速后连续不断地沿两平行金属板间的中线射入，若两板间距恰能使所有子都能通过．且两极长度使每个电子通过两板均历时3t0，电子所受重力不计，试求：
（1）电子通过两板时侧向位移的最大值和最小值；
（2）侧向位移最大和最小的电子通过两板后的动能之比。
如图所示的电路中，电源电动势E＝6V，内阻
，电阻
，
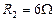，电容器的电容C=3.6μF，二极管D具有单向导电性，开始时，开关S1闭合，S2断开．
（1）合上S2，待电路稳定以后，求电容器C上电量变化了多少？
（2）合上S2，待电路稳定以后再断开S1，求断开S1后流过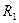
的电量是多少？
把一电荷量为＋q、质量为m的小球放在光滑水平面上，水平面上方有一方向向东的匀强电场，用手按住小球使其静止在P点，现在突然放开手，并设法使小球突然获得一水平向西的速度v，并且在小球开始运动的同时，对小球施加一水平向北、大小为F的恒力（图中未画出），当小球向西运动到最远处的速度大小也为v，求：
（1）电场强度的大小；
（2）小球向西运动的最大距离。