如图所示,质量为m=1kg的物块,放置在质量M=2kg足够长木板的中间,物块与木板间的动摩擦因数为0.1,木板放置在光滑的水平地面上.在地面上方存在两个作用区,两作用区的宽度均为1m,边界距离为d,作用区只对物块有力的作用:I作用区对物块作用力方向水平向右,II作用区对物块作用力方向水平向左.作用力大小均为3N.将物块与木板从图示位置(物块在I作用区内的最左边)由静止释放,已知在整个过程中物块不会滑离木板.取g=10m/s2.
(1)在物块刚离开I区域时,物块的速度多大?
(2)若物块刚进入II区域时,物块与木板的速度刚好相同,求两作用区的边界距离d;
(3)物块与木板最终停止运动时,求它们相对滑动的路程.
汽车前方120m有一自行车正以6m/s的速度匀速前进,汽车以18m/s的速度追赶自行车,若两车在同一条公路不同车道上作同方向的直线运动,求:
(1)经多长时间,两车第一次相遇?
(2)若汽车追上自行车后立即刹车,汽车刹车过程中的加速度大小为2m/s2,则再经多长时间两车第二次相遇?
一艘快艇以2m/s2的加速度在海面上做匀加速直线运动,快艇的初速度是4m/s。求:
(1)这艘快艇在8s末的速度;
(2)8s内经过的位移。
如图所示,质量为m=4kg的小球用细绳拴着吊在行驶的汽车后壁上,绳与竖直方向夹角为θ=37º,已知g = 10m/s2,sin37º=0.6,cos37º=0.8,求:
(1)汽车匀速运动时,细线对小球的拉力FT、车后壁对小球的压力FN这两个力的大小;
(2)当汽车以a=10m/s2向左匀加速行驶时,细线对小球的拉力(包括方向)和小球对车后壁的压力。
某人站在一平台上,用长L=0.6m的轻细线拴一个质量为m=0.6kg的小球,让它在竖直平面内以O点为圆心做圆周运动,当小球转到最高点A时,人突然撒手。经t=0.8s小球落地,落地点B与A点的水平距离x=4.8m,不计空气阻力,g=10m/s2。求:
(1)A点距地面高度h;
(2)人撒手前小球运动到A点时,绳对球的拉力FT的大小。
物体质量m= 4kg,放在倾角为θ=37º的斜面上。在沿斜面向上的拉力F = 40N作用下物体以v=6m/s的速度沿斜面向上作匀速直线运动,取g="10" m/s2,sin37º=0.6,cos37º=0.8,求: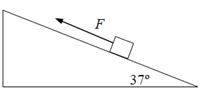
(1)物体与斜面间的动摩擦因数μ;
(2)力F撤去后,物体继续沿斜面向上运动的最大距离。