如图所示,质量为m、边长为L的正方形线框,在竖直平面内从有界的匀强磁场上方由静止自由下落.线框电阻为R,匀强磁场的宽度为H(L<H),磁感应强度为B.线框下落过程中ab边始终与磁场边界平行且水平.已知ab边刚进入磁场和刚穿出磁场时线框都立即做减速运动,且瞬时加速度大小都是 ,求:
,求:
(1)ab边刚进入磁场与ab边刚出磁场时的速度大小;
(2)线框进入磁场的过程中产生的热量.
在光滑水平面上有足够长的木板A,质量为M,在A的右端放有一个质量为m的小物块B,A、B间的动摩擦因素为μ,起初A、B均静止(如 图). 现用水平力F1作用在A上,使A先以加速度
图). 现用水平力F1作用在A上,使A先以加速度 向右做加速运动,当速度达到v0后立即改用水平力F2作用在A上,使A开始匀速运动.
向右做加速运动,当速度达到v0后立即改用水平力F2作用在A上,使A开始匀速运动. 已知在此过程中物体B在木板A上发生了滑动,但最后还是相对A静止下来.
已知在此过程中物体B在木板A上发生了滑动,但最后还是相对A静止下来.
(1)在下面的 图中定性画出A和B的速度图象;
图中定性画出A和B的速度图象;
(2)求F1与F2的比值;
(2)求出最后B离A右端的距离d.

A、B两个小物块用轻绳连结,绳跨过位于倾角为300的光滑斜面(斜面足够长)顶端的轻质滑轮,滑轮与转轴之间的摩擦不计,斜面固定在水平桌面上,如图所示.第一次,B悬空,A放在斜面上,A恰好静止;第二次,将B的质量改变,发现A自斜面顶端由静止开始运动,经时间t速度大小为v,已知物块A的质量为m,重力加速度为g,求物块B质量改变了多少?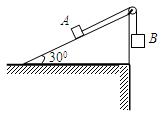
如图所示在倾角为θ=30°的斜坡顶端A处,沿水平方向以初速度v0=10m/s抛出一小球,落在斜坡的B点, ,
,
求:(1)小球在空中飞行的时间。
(2)AB间的距离。
某1kg物体在水平拉力F作用下,由静止开始在光滑水平面上做直线运动,力F随时间t变化的规律如图所示,则物体在 前4s内的位移为多少?
前4s内的位移为多少?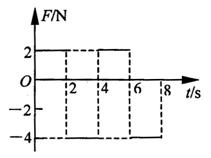
如图为某种新型设备内部电、磁场分布情况图。自上而下分为Ⅰ、Ⅱ、Ⅲ三个区域。区域Ⅰ宽度为d1,分布沿纸面向下的匀强电场E1;区域Ⅱ宽度为d2,分布垂直纸面向里的匀强磁场B1;宽度可调的区域Ⅲ中分布沿纸面向下的匀强电场E2和垂直纸面向里的匀强磁场B2。现在有一群质量和带电量均不同的带电粒子从区域Ⅰ上边缘的注入孔A点被注入,从静止开始运动,然后相继进入Ⅱ、Ⅲ两个区域,满足一定条件的粒子将回到区域Ⅰ,其他粒子则从区域Ⅲ飞出。三区域都足够长,粒子的重力不计。
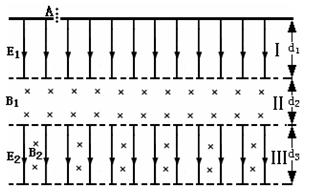
求:能飞回区域Ⅰ的粒子第一次回到区域Ⅰ上边缘时离A的距离?