如图所示，在xOy坐标系第二象限内有一圆形匀强磁场区域，半径为
，圆心O′坐标为(- , )，磁场方向垂直xOy平面。在x轴上有坐标（- ，0)的P点，两个电子a、b以相同的速率v沿不同方向从P点同时射入磁场，电子
的入射方向为y轴正方向，b的入射方向与y轴正方向夹角为
。电子a经过磁场偏转后从y轴上的 Q(0， ）点进入第一象限，在第一象限内紧邻y轴有沿y轴正方向的匀强电场，场强大小为
，匀强电场宽为
。已知电子质量为
、电荷量为
,不计重力及电子间的相互作用。求：
（1）磁场的磁感应强度B的大小
（2）b电子在磁场中运动的时间
（3）a、b两个电子经过电场后到达x轴的坐标差Δx
2011年11月3日，神舟八号飞船首次成功与天宫一号实现交会对接, 为中国航天第三步建设空间站做好了准备,实现了我国空间技术发展的重大跨越。若已知飞船在地球上空的圆轨道上运行时离地面的高度为h．地球半径为R，地球表面的重力加速度为g．求飞船在该圆轨道上运行时：速度v的大小和周期T。
速度v与第一宇宙速度的比值。
如图所示，光滑水平面上有一质量M＝4.0kg的平板车，车的上表面右侧是一段长L＝1.0m的水平轨道，水平轨道左侧连一半径R=0.25m的1/4光滑圆弧轨道，圆弧轨道与水平轨道在O/点相切．车右端固定一个尺寸可以忽略、处于锁定状态的压缩弹簧，一质量m＝1.0kg的小物块紧靠弹簧，小物块与水平轨道间的动摩擦因数μ＝0.5。整个装置处于静止状态，现将弹簧解除锁定，小物块被弹出，恰能到达圆弧轨道的最高点A，g取10m/s2．求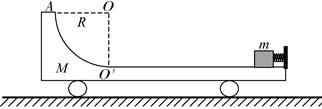
解除锁定前弹簧的弹性势能；
小物块第二次经过O/点时的速度大小；
最终小物块与车相对静止时距O/点的距离．
带电量与质量分别为q，m的离子从离子枪中水平射出，与离子枪相距d处有两平行金属板AB和CD，金属板长和宽也为d，整个空间存在一磁
感强度为B的匀强磁场如图所示。离子垂直于磁场边界中点飞入磁场，不考虑重力的作用，离子的速度应在什么范围内，离子才能打到金属板上？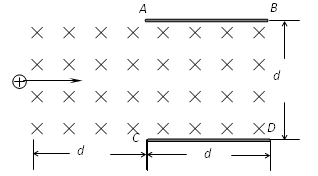
如图所示，在一半径为50cm环形绝缘光滑细管处在着垂直纸面向里的匀强磁场中，磁感应强度为2.2T，管内有一个质量为10g的带电小球以6m/s的速度从管的最低点逆时针管中运动，运动到管的最高点时恰好对管没有作用力。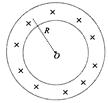
带电小球在最高点的速度为多大？
带电小球的电性，及带电量为多少？
已知地球半径为R，地表重力加速度为g，自转周期为T，求：地球同步卫星距离地面的高度。