如图所示,一固定斜面倾角为30°,一质量为m的小物块自斜面底端以一定的初速度沿斜面向上做匀减速运动,加速度大小等于重力加速度的大小g。物块上升的最大高度为H,则此过程中,物块的( )
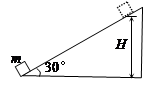
| A.动能损失了2mgH |
| B.动能损失了mgH |
| C.机械能损失了mgH |
D.机械能损失了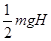 |
以下属于离心现象应用的是()
| A.离心沉淀器 |
| B.标枪运动员掷出的标枪 |
| C.家用洗衣机的甩干桶用于干燥衣物 |
| D.转动伞柄可将雨伞上的水甩出 |
如图所示,被激发的氢原子从较高能态跃迁到较低能态时,发出波长分别为λ1、λ2、λ3的三条谱线,则三者的关系是 ……()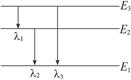
| A.λ3=λ1+λ2 | B.λ1=λ2+λ3 |
C. |
D. |
某种单色光照射到金属表面时,(如图所示)金属表面有光子逸出,如果光的强度减弱,频率不变,则下列说法正确的是()
| A.光的强度减弱到某一最低数值时,就没有光电子逸出 |
| B.单位时间内逸出的光电子数减少 |
| C.逸出光电子的最大初动能减少 |
| D.单位时间内逸出的光电子数和光电子的最大初动能都要减少 |
在光电效应实验中,下列结果正确的是()
| A.如果入射光比较弱,只要照射的时间足够长,就会产生光电效应 |
| B.当入射光的频率增大为原来的两倍时,光电子的最大初动能也增大为原来的两倍 |
| C.当入射光的波长增大为原来两倍时,可能不产生光电效应 |
| D.当入射光的强度增大为原来两倍时,单位时间发射光电子的数量也增大为原来的两倍 |
用某种单色光照射某种金属表面,发生光电效应.现将该单色光的光强减弱,则()
| A.光电子的最大初动能不变 | B.光电子的最大初动能减少 |
| C.单位时间内产生的光电子数减少 | D.可能不发生光电效应 |