1932年,劳伦斯和利文斯设计出了回旋加速器.回旋加速器的工作原理如图所示,置于真空中的两个D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计.磁感应强度为B的匀强磁场与盒面垂直. 设两D形盒之间所加的交流电压为U,被加速的粒子质量为m、电量为q,粒子从D形盒一侧开始被加速(初动能可以忽略),经若干次加速后粒子从D形盒边缘射出.
求:(1)粒子从静止开始第1次经过两D形盒间狭缝加速后的速度大小
(2)粒子第一次进入D型盒磁场中做圆周运动的轨道半径
(3)粒子至少经过多少次加速才能从回旋加速器D形盒射出
如图所示,水平传送带AB长L=8.3m,质量为M=1kg的木块随传送带一起以v1=2m/s的速度向左匀速运动(传送带的传送速度恒定),木块与传送带间的动摩擦因数μ=0.5.当木块运动至最左端A点时,一颗质量为m=20g的子弹以v0=300m/s水平向右的速度正对射入木块并穿出,穿出时速度u=50m/s,以后每隔1s就有一颗同样的子弹射向木块,设子弹射穿木块的时间极短,且每次射入点各不相同,木块的质量保持不变,g取10m/s2.求:
(1)在被第二颗子弹击中前,木块向右运动离A点的最大距离?
(2)从第一颗子弹射中木块到木块刚要被第二颗子弹击中的过程中,子弹、木块和传送带这一系统产生的热能是多少?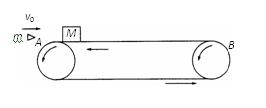
天文学家测得银河系中氦的含量约为25%。有关研究表明,宇宙中氦生成的途径有两条:一是在宇宙诞生后2分钟左右生成的;二是在宇宙演化到恒星诞生后,由恒星内部的氢核聚变反应生成的。
(1)4个氢核( H)聚变成1个氦核(
H)聚变成1个氦核( He),同时放出2个正电子(
He),同时放出2个正电子( e)和2个中微子(ν0),请写出该氢核聚变反应的方程,并计算一次反应释放的能量。
e)和2个中微子(ν0),请写出该氢核聚变反应的方程,并计算一次反应释放的能量。
(2)研究表明,银河系的年龄约为t=3.8×1017s,每秒银河系产生的能量约为1×1037J(P=1×1037J/s),现假定该能量全部来自上述氢核聚变反应,试估算银河系中氦的含量(最后结果保留2位有效数字)
(3)根据你的估算结果,对银河系中氦的主要生成途径作出判断。
(可能用到的数据:银河系的质量约为M=3×1041kg,原子质量单位1u=1.66×10 kg,1u相当于1.5×10
kg,1u相当于1.5×10 J的能量,电子质量me=0.0005u,氦核质量mα=4.0026u,氢核质量mp=1.0078u,中微子ν0质量为零。
J的能量,电子质量me=0.0005u,氦核质量mα=4.0026u,氢核质量mp=1.0078u,中微子ν0质量为零。
如图所示,光滑水平面上有A、B、C三个物块,质量分别为mA = 2.0kg,mB = 1.0kg,mC = 1.0kg.现用一轻弹簧将A、B两物块连接,并用力缓慢压缩弹簧使A、B两物块靠近,此过程外力做108J的功(弹簧仍处于弹性限度内),然后同时释放A、B,弹簧开始逐渐变长,当弹簧刚好恢复原长时,C恰以4m/s的速度迎面与B发生碰撞并粘连在一起.求:
(1)弹簧刚好恢复原长时(B与C碰撞前)A和B物块速度的大小.
(2)当弹簧第二次被压缩时,弹簧具有的最大弹性势能.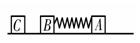
如图所示,质量mA="4.0" kg的木板A放在光滑的水平面C上,木板右端放着质量mB="1.0" kg的小物块B(视为质点),小物块与木板间的动摩擦因数μ=0.24.开始时,它们均处于静止状态,现在木板A突然受到一个水平向右的12 N·s的瞬时冲量I作用开始运动.假设木板足够长,重力加速度g取10 m/s2.求:
(1)瞬时冲量作用结束时木板的速度v0;
(2)小物块B从开始运动到相对木板静止的过程中对地发生的位移.
云室处在磁感应强度为B的匀强磁场中,一静止的质量为M的原子核在云室中发生一次α衰变,α粒子的质量为m,电量为q,其运动轨迹在与磁场垂直的平面内.现测得α粒子运动的轨道半径R,试求在衰变过程中的质量亏损.(注:涉及动量问题时,亏损的质量可忽略不计.)