能的转化与守恒是自然界普遍存在的规律，如：电源给电容器的充电过程可以等效为将电荷逐个从原本电中性的两极板中的一个极板移到另一个极板的过程. 在移动过程中克服电场力做功，电源的电能转化为电容器的电场能．实验表明:电容器两极间的电压与电容器所带电量如图所示．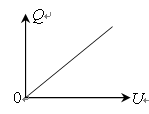
（1）对于直线运动，教科书中讲解了由v-t图像求位移的方法．请你借鉴此方法，根据图示的Q-U图像，若电容器电容为C，两极板间电压为U，求电容器所储存的电场能．
（2）如图所示，平行金属框架竖直放置在绝缘地面上．框架上端接有一电容为C的电容器．框架上一质量为m、长为L的金属棒平行于地面放置，离地面的高度为h．磁感应强度为B的匀强磁场与框架平面相垂直．现将金属棒由静止开始释放，金属棒下滑过程中与框架接触良好且无摩擦．开始时电容器不带电，不计各处电阻．
求a. 金属棒落地时的速度大小
b. 金属棒从静止释放到落到地面的时间
一艘宇宙飞船飞近某一新发现的行星，并进入靠近该行星表面的圆形轨道绕行数圈后，着陆在该行星上。飞船上备有以下实验器材：①精确秒表一只；②已知质量为
的物体一个；③弹簧测力计一个。若宇航员在绕行时测出了飞船绕行星运行的周期为T，着陆后质量为的物体所受重力为F。并已知万有引力常量为G，行星的自转可忽略不计，试求出该星球的半径R及星球的质量M。
一位质量为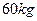
的运动员用
的时间跑完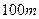
路程。设他从开始起跑的前4.0s时间作的是匀加速直线运动，后8.0s时间则作匀速直线运动，速度大小等于第4.0s末时的瞬时速度。已知他在整个运动过程中受到的阻力保持不变，大小为72N。求他在跑这100m过程中做功的平均功率；
他的瞬时功率的最大值。
如图所示，一物体从光滑斜面顶端由静止开始下滑。已知物体的质量
，斜面的倾角
，斜面长度
，重力加速度取
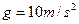。求：
物体滑到斜面底端时重力对物体做功的瞬时功率。
物体下滑的全过程中重力做功的平均功率。
物体下滑的全过程中斜面的支持力对物体的冲量大小。
如图所示，一个质量为
的垒球，以
的水平速度飞向球棒，被球棒打击后反向水平飞回，速度大小变为
，设球棒与垒球的作用时间为
。求：球棒对垒球的平均作用力大小；
球棒对垒球做的功
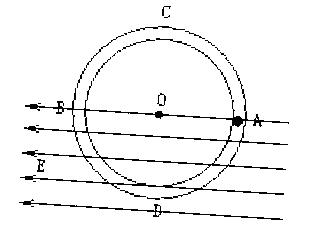
如图，半径为R的环形塑料管固定在竖直面放置，AB为管的水平直径，管的粗细远小于管的半径，AB及其以下部分处于水平向左的匀强电场中，管的内壁光滑，现将一质量为m、带正电小球从管中A点静止释放，已知小球受到的重力与它受到的电场力相等，重力加速度为g，则释放后：求小球第一次经过最低点D时的速率；
小球第二次经过最高点C时，管壁对小球的作用力？
