如图，两块相同平板P1、P2置于光滑水平面上，质量均为m。P2的右端固定一轻质弹簧，左端A与弹簧的自由端B相距L。物体P置于P1的最右端，质量为2m且可以看作质点。P1与P以共同速度v0向右运动，与静止的P2发生碰撞，碰撞时间极短，碰撞后P1与P2粘连在一起，P压缩弹簧后被弹回并停在A点（弹簧始终在弹性限度内）。P与P2之间的动摩擦因数为μ，求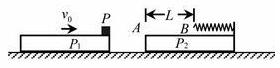
(1) P1、P2刚碰完时的共同速度v1和P的最终速度v2；
(2) 此过程中弹簧最大压缩量x和相应的弹性势能Ep
一颗人造地球卫星绕地球做匀速圆周运动，卫星离地面的高度为h。已知地球半径为R，地面重力加速度为g。求：
（1）卫星的线速度；
（2）卫星的周期。
如图所示，某人在山上将一质量m=0.50kg的石块，以v0=5.0m／s的初速度斜向上方抛出，石块被抛出时离水平地面的高度h=10m。不计空气阻力，取g=10m/s2。求：
（1）石块从抛出到落地的过程中减少的重力势能；
（2）石块落地时的速度大小。
为了迎接太空时代的到来，美国国会通过一项计划：在2050年前建造成太空升降机，就是把长绳的一端搁置在地球的卫星上，另一端系住长降机。放开绳，升降机能到达地球上；人坐在升降机里，在卫星上通过电动机把升降机拉到卫星上。已知地球表面的重力加速
，地球半径为
。求：
（1）某人在地球表面用体重计称得重180N，站在升降机中，当升降机以加速度
（
为地球表面处的重力加速度）竖直上升时，在某处此人再一次用同一体重计称得视重为170N，忽略地球自转的影响，求升降机此时距地面的高度；
（2）如果把绳的一端搁置在同步卫星上，地球自转的周期为
，求绳的长度至少为多长。
长为0.5m，质量可忽略的杆，其下端固定于O点，上端连有质量m=2kg的小球，它绕O点做圆周运动，当通过最高点时，如图所示，求下列情况下，杆受到的力（说明是拉力还是压力）：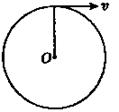
（1）当v1=1m/s时；
（2）v2=4m/s时。（g取10m/s2）
现代观测表明，由于引力作用，恒星有“聚集”的特点。众多的恒星组成不同层次的恒星系统，最简单的恒星系统是两颗互相绕转的双星，如图所示，两星各以一定速率绕其连线上某一点匀速转动，这样才不至于因万有引力作用而吸引在一起。已知双星质量分别为m1、m2，它们间的距离始终为L，引力常量为G，求：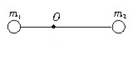
(1)双星旋转的中心O到m1的距离；
(2)双星的转动角速度。