若已知行星绕太阳公转的半径为r，公转的周期为T，万有引力恒量为G，则由此可求出（ ）
| A．某行星的质量 | B．太阳的质量 |
| C．某行星的密度 | D．太阳的密度 |
如图5所示，一轻弹簧固定于O点，另一端系一重物，将重物从与悬点O在同一水平面且弹簧保持原长的A点无初速地释放，让它自由摆下，不计空气阻力，在重物由A点摆向最低点的过程中（）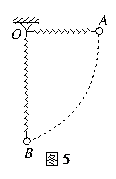
| A．重物的重力势能减少 | B．重物的重力势能增大 |
| C．重物的机械能不变 | D．重物的机械能减少 |
质量为m的物体，由静止开始下落，由于阻力作用，下落的加速度为
g，在物体下落h的过程中，下列说法中正确的应是（）
| A．物体的动能增加了mgh |
| B．物体的机械能减少了mgh |
C．物体克服阻力所做的功为 mgh |
| D．物体的重力势能减少了mgh |
质量为m的小球用长为L的轻绳悬于O点，如图4所示，小球在水平力F作用下由最低点P缓慢地移到Q点，在此过程中F做的功为（）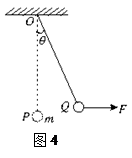
| A．FLsinθ | B．mgLcosθ |
| C．mgL（1－cosθ） | D．FLtanθ |
如图3所示，质量为m的木块放在光滑的水平桌面上，用轻绳绕过桌边的定滑轮与质量为M的砝码相连，已知M=2m，让绳拉直后使砝码从静止开始下降h（小于桌面）的距离，木块仍没离开桌面，则砝码的速率为（）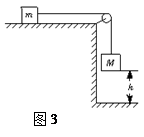
A．  |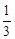
B． |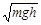
C． |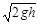
D． |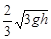
物体从高处自由下落，若选地面为参考平面，则下落时间为落地时间的一半时，物体所具有的动能和重力势能之比为（）
| A．1:4 | B．1:3 | C．1:2 | D．1:1 |