土星周围有许多大小不等的岩石颗粒,其绕土星的运动可视为圆周运动。其中有两个岩石颗粒A和B与土星中心距离分别为rA=8.0×104 km和r B=1.2×105 km。忽略所有岩石颗粒间的相互作用。(结果可用根式表示)
(1)求岩石颗粒A和B的线速度之比;
(2)求岩石颗粒A和B的周期之比;
(3)土星探测器上有一物体,在地球上重为10 N,推算出他在距土星中心3.2×105 km处受到土星的引力为0.38 N。已知地球半径为6.4×103 km,请估算土星质量是地球质量的多少倍?
有一个竖直固定在地面的透气圆筒,筒中有一劲度系数为 的轻弹簧,其下端固定,上端连接一质量为
的轻弹簧,其下端固定,上端连接一质量为 的薄滑块,圆筒内壁涂有一层新型智能材料─—ER流体,它对滑块的阻力可调。起初,滑块静止,ER流体对其阻力为0,弹簧的长度为L.现有一质量也为
的薄滑块,圆筒内壁涂有一层新型智能材料─—ER流体,它对滑块的阻力可调。起初,滑块静止,ER流体对其阻力为0,弹簧的长度为L.现有一质量也为 的物体从距地面2L处自由落下,与滑块碰撞后粘在一起向下运动。为保证滑块做匀减速运动,且下移距离为
的物体从距地面2L处自由落下,与滑块碰撞后粘在一起向下运动。为保证滑块做匀减速运动,且下移距离为 时速度减为0,ER流体对滑块的阻力须随滑块下移而变。试求(忽略空气阻力):
时速度减为0,ER流体对滑块的阻力须随滑块下移而变。试求(忽略空气阻力):
(1)下落物体与滑块碰撞前的瞬间物体的速度;
(2)下落物体与滑块碰撞过程中系统损失的机械能;
(3)滑块下移距离d时ER流体对滑块阻力的大小。
一质量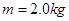 的小物块以一定的初速度冲上一足够长的斜面,斜面的倾角
的小物块以一定的初速度冲上一足够长的斜面,斜面的倾角 .某同学利用传感器测出了小物块从一开始冲上斜面上滑过程中多个时刻的瞬时速度,并用计算机作出了小物块上滑过程的速度—时间图线,如图所示.(已知重力加速度
.某同学利用传感器测出了小物块从一开始冲上斜面上滑过程中多个时刻的瞬时速度,并用计算机作出了小物块上滑过程的速度—时间图线,如图所示.(已知重力加速度 ,
, ,
,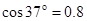 )求:
)求: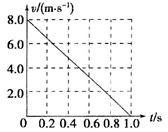
(1)小物块冲上斜面过程中加速度的大小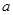 ;
;
(2)小物块与斜面间的动摩擦因数 ;
;
(3)小物块沿斜面上滑的过程中克服摩擦阻力做的功 .
.
如图所示,两平行金属板A、B长8cm,两板间距离d=8cm,A板比B板电势高300V,一带正电的粒子电荷量q=10-10C,质量m=10-20kg,不计粒子的重力作用,沿电场中心线RO垂直电场线飞入电场,初速度υ0=2×106m/s,粒子飞出平行板电场后经过界面MN、PS间的无电场区域后,进入固定在O点的点电荷Q形成的电场区域,(设界面PS右边点电荷的电场分布不受界面的影响),已知两界面MN、PS相距为12cm,D是中心线RO与界面PS的交点,O点在中心线上,距离界面PS为9cm,粒子穿过界面PS最后垂直打在放置于中心线上的荧光屏bc上.(静电力常数k = 9.0×109N·m2/C2)
(1)求粒子穿过界面MN时偏离中心线RO的距离多远?
(2)到达PS界面时离D点多远?
(3)确定点电荷Q的带电性质并求其电荷量的大小。
如图1所示,质量m=1.0kg的物块,在水平向右、大小F = 5.0N的恒力作用下,沿足够长的粗糙水平面由静止开始运动。在运动过程中,空气对物块的阻力沿水平方向向左,其大小f空=kv,k为比例系数,f空随时间t变化的关系如图2所示。g取10m/s2。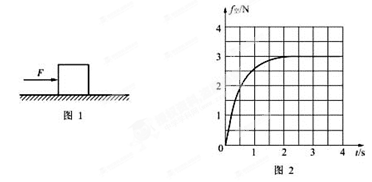
(1)求物块与水平面间的动摩擦因数μ;
(2)估算物块运动的最大速度vm;
(3)估算比例系数k。
如图所示,倾角为37°的粗糙斜面AB底端与半径R=0.4m的光滑半圆轨道BC平滑相连,O为轨道圆心,BC为圆轨道直径且处于竖直方向,A、C两点等高。质量m=1kg的滑块从A点由静止开始下滑,恰能滑到与O等高的D点,(g取10m/s2,sin37º=0.6, cos37º=0.8)
(1)求滑块与斜面间的动摩擦因数μ。
(2)若使滑块能到达C点,求滑块从A点沿斜面滑下时的初速度v0的最小值。
(3)若滑块离开A处的速度大小为 m/s,求滑块从C点飞出至落到斜面上的时间t。
m/s,求滑块从C点飞出至落到斜面上的时间t。