已知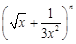 的第五项的二项式系数与第三项的二项式系数的比是
的第五项的二项式系数与第三项的二项式系数的比是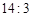 ,求展开式中不含x的项.
,求展开式中不含x的项.
复平面内有A、B、C三点,点A对应复数是3+i,向量 对应复数是-2-4i,向量
对应复数是-2-4i,向量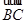 表示的复数是-4-i,求B点对应复数.
表示的复数是-4-i,求B点对应复数.
计算由曲线 与直线
与直线 所围成图形的面积。
所围成图形的面积。
在气象台A正西方向300千米处有一台风中心,它以每小时40千米的速度向东北方向移动,距台风中心250千米以内的地方都要受其影响。问:从现在起,大约多长时间后,气象台A所在地将遭受台风影响?持续多长时间?
(注: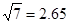 ,
,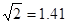 )
)
为调查某地区老年人是否需要志愿者提供帮助用简单随机抽样方法从该地区调查了500位老年人,
结果如下:
| 男 |
女 |
|
| 需要 |
40 |
30 |
| 不需要 |
160 |
270 |
(1)估计该地区老年人中需要志愿者提供帮助的老年人的比例
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?