已知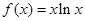 ,
,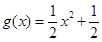 .
.
(1)设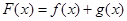 ,求函数
,求函数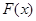 的图像在
的图像在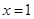 处的切线方程;
处的切线方程;
(2)求证: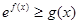 对任意的
对任意的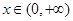 恒成立;
恒成立;
(3)若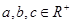 ,且
,且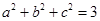 ,求证:
,求证: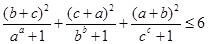 .
.
在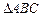 中,已知
中,已知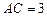 ,
,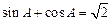 .
.
(Ⅰ)求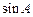 的值;
的值;
(Ⅱ)若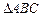 的面积
的面积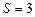 ,求
,求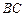 的值.
的值.
设△ABC的内角A、B、C的对边长分别为a、b、c,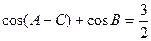 ,
, ,求B.
,求B.
在△ABC中,a, b, c分别为内角A, B, C的对边,且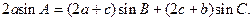
(1)求A的大小;(2)求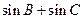 的最大值.
的最大值.
(本小题满分13分)
已知函数 是定义在
是定义在 上的奇函数,当
上的奇函数,当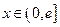 时,
时, 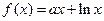 (其中e是自然对数的底,
(其中e是自然对数的底,  )
)
(1)求 的解析式;
的解析式;
(2)设 ,求证:当
,求证:当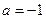 时,
时,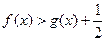 ;
;
(3)是否存在实数a,使得当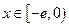 时,
时, 的最小值是3 ?如果存在,求出实数a的值;如果不存在,请说明理由。
的最小值是3 ?如果存在,求出实数a的值;如果不存在,请说明理由。
(本小题满分13分)
已知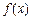 是定义在[-1,1]上的奇函数,且
是定义在[-1,1]上的奇函数,且 ,若任意的
,若任意的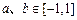 ,当
,当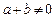 时,总有
时,总有 .
.
(1)判断函数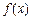 在[-1,1]上的单调性,并证明你的结论;
在[-1,1]上的单调性,并证明你的结论;
(2)解不等式: ;
;
(3)若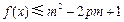 对所有的
对所有的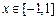 恒成立,其中
恒成立,其中 (
(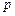 是常数),试用常数
是常数),试用常数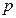 表示实数
表示实数 的取值范围.
的取值范围.