已知数列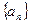 的前
的前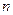 项和
项和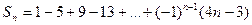 ,
,
(1)求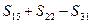 的值。(2)求
的值。(2)求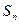 的表达式
的表达式
已知 、
、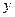 满足约束条件
满足约束条件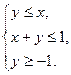
(1)求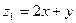 的最小值,以及相应的
的最小值,以及相应的 、
、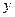 值;
值;
(2)求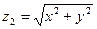 的最大值,以及相应的
的最大值,以及相应的 、
、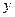 值
值
一缉私艇发现在北偏东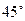 方向,距离12 nmile的海面上有一走私船正以10 nmile/h的速度沿东偏南
方向,距离12 nmile的海面上有一走私船正以10 nmile/h的速度沿东偏南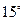 方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东
方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东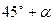 的方向去追,.求追击所需的时间和
的方向去追,.求追击所需的时间和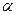 角的正弦值.
角的正弦值.
在△ABC中,BC=a,AC=b,a,b是方程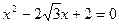 的两个根,且
的两个根,且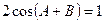 。
。
求:(1)角C的度数;
(2)AB的长度。
设{an}是正数组成的数列,其前n项和为Sn,并且对于所有的n N+,都有
N+,都有 。
。
(1)写出数列{an}的前3项;
(2)求数列{an}的通项公式(写出推证过程);
(3)设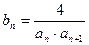 ,
, 是数列{bn}的前n项和,求使得
是数列{bn}的前n项和,求使得 对所有n
对所有n N+都成立的最小正整数
N+都成立的最小正整数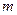 的值。
的值。