已知椭圆 的长轴长为
的长轴长为 ,离心率为
,离心率为 ,
, 分别为其左右焦点.一动圆过点
分别为其左右焦点.一动圆过点 ,且与直线
,且与直线 相切.
相切.
(1)(ⅰ)求椭圆 的方程;(ⅱ)求动圆圆心轨迹
的方程;(ⅱ)求动圆圆心轨迹 的方程;
的方程;
(2)在曲线 上有四个不同的点
上有四个不同的点 ,满足
,满足 与
与 共线,
共线, 与
与 共线,且
共线,且 ,求四边形
,求四边形 面积的最小值.
面积的最小值.
如图,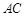 是圆
是圆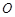 的直径,点
的直径,点 在圆
在圆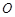 上,
上,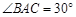 ,
,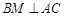 交
交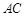 于点
于点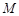 ,
,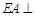 平面
平面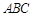 ,
,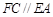 ,
,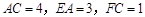 .
.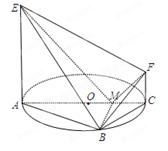
(1)证明: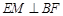 ;
;
(2)求平面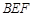 与平面
与平面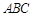 所成的锐二面角的大小.
所成的锐二面角的大小.
已知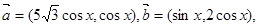 设函数
设函数
(Ⅰ)当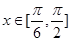 ,求函数
,求函数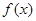 的的值域;
的的值域;
|
(Ⅱ)当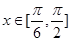 时,若
时,若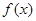 ="8," 求函数
="8," 求函数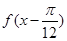 的值;
的值;
已知函数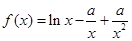 (
(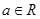 ).
).
(1)若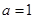 ,求函数
,求函数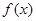 的极值;
的极值;
(2)若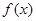 在
在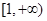 内为单调增函数,求实数a的取值范围;
内为单调增函数,求实数a的取值范围;
(3)对于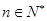 ,求证:
,求证: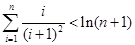 .
.
设椭圆C: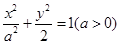 的左、右焦点分别为F1、F2,A是椭圆C上的一点,
的左、右焦点分别为F1、F2,A是椭圆C上的一点,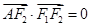 ,坐标原点O到直线AF1的距离为
,坐标原点O到直线AF1的距离为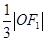 .
.
(1)求椭圆C的方程;
(2)设Q是椭圆C上的一点,过点Q的直线l 交 x 轴于点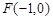 ,交 y 轴于点M,若
,交 y 轴于点M,若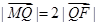 ,求直线l 的斜率.
,求直线l 的斜率.
已知{an}为递增的等比数列,且{a1,a3,a5}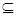 {-10,-6,-2,0,1,3,4,16}.
{-10,-6,-2,0,1,3,4,16}.
(1)求数列{an}的通项公式;
(2)是否存在等差数列{bn},使得a1bn+a2bn-1+a3bn-2+…+anb1=2n+1-n-2对一切n∈N*都成立?若存在,求出bn;若不存在,说明理由.