平面直角坐标中，已知点O（0，0），A（0，2），B（1，0），点P是反比例函数y=﹣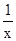
图象上的一个动点，过点P作PQ⊥x轴，垂足为Q．若以点O、P、Q为顶点的三角形与△OAB相似，则相应的点P共有（ ）
| A．1个 | B．2个 | C．3个 | D．4个 |
已知
、
是一元二次方程
的两个根，则
等于（）
A． |
B． |
C．1 | D．4 |
sin30°的值是（）
| A．1 | B． |
C． |
D． |
点P是△ABC内（不在边上）一点，连接PA、PB、PC，如果△PAB、△PBC、△PAC中存在一个三角形与原△ABC相似，那么我们把点P叫做△ABC的内相似点．已知在Rt△ABC中，∠ACB=90°，AC=3，BC= 4，若点P是△ABC的内相似点，则cos∠PAB的值为（）
A．
B．
C．
D．
如图1，在平面内选一定点O，引一条有方向的射线Ox，再选定一个单位长度，那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定，有序数对（θ，m）称为M点的“极坐标”，这样建立的坐标系称为“极坐标系”．应用：在图2的极坐标系下，如果正六边形的边长为2，有一边OA在射线Ox上，则正六边形的顶点C的极坐标应记为（）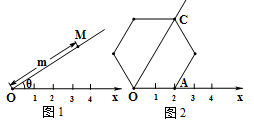
| A．（60°，4） | B．（45°，4） | C．（60°， ） |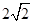
D．（50°，） |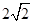
若关于x的一元二次方程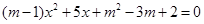
的常数项为0，则m的值等于（ ）
| A．1 | B．2 | C．1或2 | D．0 |