勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,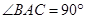 ,
, ,
,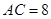 ,点
,点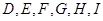 都是矩形
都是矩形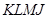 的边上,则矩形
的边上,则矩形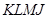 的面积为( )
的面积为( )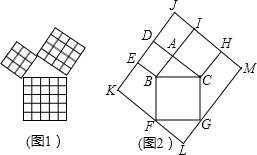
A.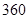 |
B.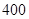 |
C.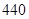 |
D.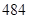 |
学校为创建"书香校园",购买了一批图书.已知购买科普类图书花费10000元,购买文学类图书花费9000元,其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元,且购买科普书的数量比购买文学书的数量少100本.求科普类图书平均每本的价格是多少元?若设科普类图书平均每本的价格是 x元,则可列方程为( )
| A. |
﹣ =100 |
B. |
﹣ =100 |
| C. |
﹣ =100 |
D. |
﹣ =100 |
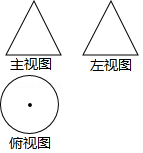
如图,一个几何体的主视图和左视图都是边长为6的等边三角形,俯视图是直径为6的圆,则此几何体的全面积是( )
| A. |
18π |
B. |
24π |
C. |
27π |
D. |
42π |
小刚从家去学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车匀速行驶一段时间后到达学校,小刚从家到学校行驶路程 s(单位: m)与时间 t(单位: min)之间函数关系的大致图象是( )
| A. |
|
B. |
|
| C. |
|
D. |
|
下列说法错误的是( )
| A. |
通过平移或旋转得到的图形与原图形全等 |
| B. |
"对顶角相等"的逆命题是真命题 |
| C. |
圆内接正六边形的边长等于半径 |
| D. |
"经过有交通信号灯的路口,遇到红灯"是随机事件 |
剪纸是我国传统的民间艺术,下列剪纸作品中既不是轴对称图形,也不是中心对称图形的是( )
| A. |
|
B. |
|
| C. |
|
D. |
|