如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“好玩三角形”．
（1）请用直尺和圆规画一个“好玩三角形”；
（2）如图1，在Rt△ABC中，∠C=90°，tanA= 
，求证：△ABC是“好玩三角形”；
（3）如图2，已知菱形ABCD的边长为a，∠ABC=2β，点P，Q从点A同时出发，以相同速度分别沿折线AB﹣BC和AD﹣DC向终点C运动，记点P经过的路程为s．
①当β=45°时，若△APQ是“好玩三角形”，试求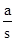
的值；
②当tanβ的取值在什么范围内，点P，Q在运动过程中，有且只有一个△APQ能成为“好玩三角形”．请直接写出tanβ的取值范围．
（4）依据（3）的条件，提出一个关于“在点P，Q的运动过程中，tanβ的取值范围与△APQ是‘好玩三角形’的个数关系”的真命题（“好玩三角形”的个数限定不能为1）